《2025年通城学典课时作业本七年级数学下册人教版》

16. 有下列命题：① 有且只有一条直线平行于已知直线；② 过直线外一点到这条直线的垂线段就是这点到直线的距离；③ 在同一平面内，互相垂直的两条线段一定相交；④ 若直线l外一点P与直线l上各点连接而成的所有线段中，最短线段的长为3 cm，则点P到直线l的距离为3 cm. 其中，错误的有 （ ）
A. 1个 B. 2个 C. 3个 D. 4个

答案： C

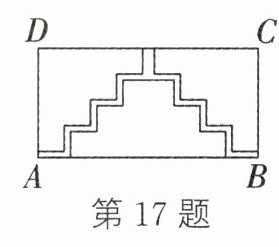
17. 如图所示为一块长方形场地的示意图，长AB为102 m，宽AD为51 m，A，B两处入口的路宽都为1 m，两条小路汇合处的路宽为2 m，其余部分为草坪，则草坪的面积为 （ ）
A. 5 050 m² B. 5 000 m² C. 1 020 m² D. 499 m²

答案： B

18. 如图，∠ABD = ∠CDB，请写出图中另外一组相等的角：________________（只能用图中的字母表示）.

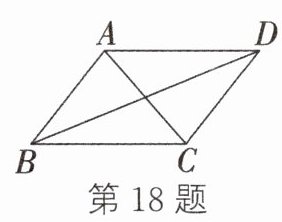
答案： ∠BAC = ∠ACD

19. 如图，AB//CD，EF//GH，∠3 = ∠4. 若∠2 = 70°，则∠1的度数为________.

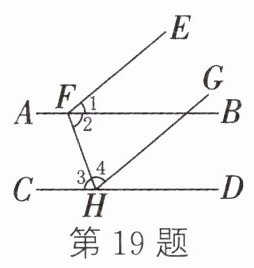
答案： 40°

20. 将一张长方形纸片折叠成如图所示的图形. 若∠ABC = 26°，则∠ACD的度数是________.

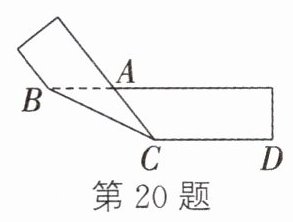
答案： 128°

21. 如图，沿虚线剪去长方形纸片相邻的两个角，使∠1 = 120°，AB⊥BC，则∠2 = ________.

答案： 150°

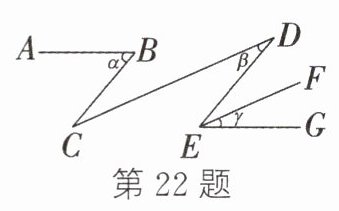
22. 如图，AB//EG，CD//EF，BC//DE，若∠α = 50°，∠β = 26°，则∠γ的度数为________.

答案：
$24° $解析：如图，延长$ AB $交$ DE $于点$ H。$因为$ BC//DE，$$∠α = 50°，$所以$∠BHE = ∠α = 50°。$因为$ CD//EF，$$∠β = 26°，$所以$∠DEF = ∠β = 26°。$因为$ AB//EG，$所以$∠HEG = ∠BHE = 50°。$所以$∠γ = ∠DEG - ∠DEF = 50° - 26° = 24°。$
$　　　　　　$

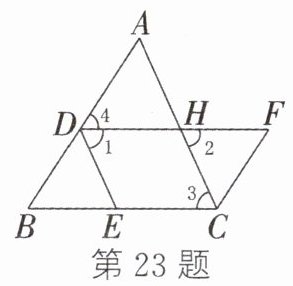
23. 如图，点D，E，H分别在三角形ABC的边AB，BC，AC上，连接DE，过点C作CF交DH的延长线于点F且满足∠B + ∠BCF = 180°. 若DE//AC，∠1 = ∠3，求证：∠B = ∠F.
证明：∵ DE//AC（已知），
∴ ∠1 = ________（两直线平行，同位角相等）.
∵ ∠1 = ∠3（已知），
∴ ∠3 = ∠2（______________）.
∴ DF//BC（____________________）.
∴ ∠4 = ∠B（两直线平行，同位角相等）.
∵ ∠B + ∠BCF = 180°（已知），
∴ ________//________（同旁内角互补，两直线平行）.
∴ ∠4 = ________（两直线平行，内错角相等）.
∴ ∠B = ∠F（等式的基本事实）.

答案： ∠2 等式的基本事实 内错角相等，两直线平行 AB CF ∠F

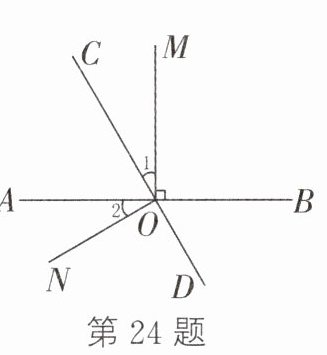
24. 如图，直线AB，CD相交于点O，OM⊥AB于点O.
（1）若∠1 = ∠2，求∠NOD的度数；
（2）若∠BOC = 4∠1，求∠AOC与∠MOD的度数.

答案：
(1) 因为 OM⊥AB，所以∠AOM = 90°。所以∠1 + ∠AOC = 90°。因为∠1 = ∠2，所以∠2 + ∠AOC = 90°。所以∠NOC = 90°。所以∠NOD = 180° - ∠NOC = 180° - 90° = 90°。
(2) 因为 OM⊥AB，所以∠AOM = ∠BOM = 90°。因为∠BOC = 4∠1，所以∠BOM = 3∠1，即 3∠1 = 90°。所以∠1 = 30°。所以∠AOC = ∠AOM - ∠1 = 90° - 30° = 60°，∠MOD = 180° - ∠1 = 180° - 30° = 150°。