第33页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
25. 中华文化博大精深,方块文字智慧灵秀,奥妙无穷. 如图①是一个“互”字,如图②是由图①抽象的几何图形,其中AB//CD,MG//FN,点E,M,F在同一条直线上,点G,N,H在同一条直线上,且∠EFN = ∠G.
(1)EF与GH平行吗?请说明理由.
(2)求证:∠AEF = ∠GHD.

(1)EF与GH平行吗?请说明理由.
(2)求证:∠AEF = ∠GHD.

答案:
(1) 平行。理由:因为 MG//FN,所以∠EFN = ∠EMG。因为∠EFN = ∠G,所以∠G = ∠EMG。所以 EF//GH。
(2) 如图,延长 EF 交 CD 于点 P。因为 AB//CD,所以∠BEF + ∠MPH = 180°。因为 EP//GH,所以∠GHP + ∠MPH = 180°。所以∠BEF = ∠GHP。因为∠BEF = 180° - ∠AEF,∠GHP = 180° - ∠GHD,所以∠AEF = ∠GHD。

(1) 平行。理由:因为 MG//FN,所以∠EFN = ∠EMG。因为∠EFN = ∠G,所以∠G = ∠EMG。所以 EF//GH。
(2) 如图,延长 EF 交 CD 于点 P。因为 AB//CD,所以∠BEF + ∠MPH = 180°。因为 EP//GH,所以∠GHP + ∠MPH = 180°。所以∠BEF = ∠GHP。因为∠BEF = 180° - ∠AEF,∠GHP = 180° - ∠GHD,所以∠AEF = ∠GHD。

$26. $已知$AB//CD.$
$(1)$如图$①,$请探索$∠A,$$∠E,$$∠C$三个角之间的数量关系,并说明理由$.$
$(2)$若$∠A = 24°.$
$① $如图$②,$若$∠F = 100°,$求$∠C + ∠E$的度数;
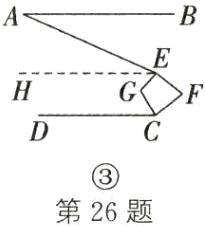
$② $如图$③,$若$∠AEF$和$∠DCF$的平分线交于点$G,$请直接写出$∠G$与$∠F$的数量关系$.$

$(1)$如图$①,$请探索$∠A,$$∠E,$$∠C$三个角之间的数量关系,并说明理由$.$
$(2)$若$∠A = 24°.$
$① $如图$②,$若$∠F = 100°,$求$∠C + ∠E$的度数;
$② $如图$③,$若$∠AEF$和$∠DCF$的平分线交于点$G,$请直接写出$∠G$与$∠F$的数量关系$.$

答案:
(1) ∠AEC + ∠C - ∠A = 180°。理由:如图①,过点 E 作 EM//AB。因为 AB//CD,所以 AB//EM//CD。所以∠AEM = ∠A,∠MEC + ∠C = 180°。所以∠AEM + ∠MEC + ∠C = ∠A + 180°,即∠AEC + ∠C - ∠A = 180°。
(2) ① 如图②,过点 F 作 FN//AB。因为 AB//CD,所以 AB//FN//CD。所以∠C + ∠NFC = 180°。所以∠C = 180° - ∠NFC。由
(1),得∠E + ∠EFN - ∠A = 180°,所以∠E = 180° - ∠EFN + ∠A。所以∠C + ∠E = 180° - ∠NFC + (180° - ∠EFN + ∠A),即∠C + ∠E = 360° - (∠NFC + ∠EFN) + ∠A = 360° - ∠EFC + ∠A。因为∠EFC = 100°,∠A = 24°,所以∠C + ∠E = 360° - 100° + 24° = 284°。
② ∠G + $\frac{1}{2}$∠F = 168°。解析:因为 EG 为∠AEF 的平分线,CG 为∠DCF 的平分线,所以∠AEG = ∠GEF,∠DCG = ∠GCF。如图③,过点 E 作 EH//AB。因为 AB//CD,所以 EH//CD,∠AEH = ∠A = 24°。设∠HEG = x°,∠DCG = y°,则易得∠G = x° + y°,∠GEF = x° + 24°,∠GCF = y°。又因为易知∠HEF + ∠F + ∠FCD = 360°,∠HEF = 2x° + 24°,∠FCD = 2y°,所以 2x° + 24° + ∠F + 2y° = 360°。所以 2∠G + ∠F = 336°。所以∠G + $\frac{1}{2}$∠F = 168°。

(1) ∠AEC + ∠C - ∠A = 180°。理由:如图①,过点 E 作 EM//AB。因为 AB//CD,所以 AB//EM//CD。所以∠AEM = ∠A,∠MEC + ∠C = 180°。所以∠AEM + ∠MEC + ∠C = ∠A + 180°,即∠AEC + ∠C - ∠A = 180°。
(2) ① 如图②,过点 F 作 FN//AB。因为 AB//CD,所以 AB//FN//CD。所以∠C + ∠NFC = 180°。所以∠C = 180° - ∠NFC。由
(1),得∠E + ∠EFN - ∠A = 180°,所以∠E = 180° - ∠EFN + ∠A。所以∠C + ∠E = 180° - ∠NFC + (180° - ∠EFN + ∠A),即∠C + ∠E = 360° - (∠NFC + ∠EFN) + ∠A = 360° - ∠EFC + ∠A。因为∠EFC = 100°,∠A = 24°,所以∠C + ∠E = 360° - 100° + 24° = 284°。
② ∠G + $\frac{1}{2}$∠F = 168°。解析:因为 EG 为∠AEF 的平分线,CG 为∠DCF 的平分线,所以∠AEG = ∠GEF,∠DCG = ∠GCF。如图③,过点 E 作 EH//AB。因为 AB//CD,所以 EH//CD,∠AEH = ∠A = 24°。设∠HEG = x°,∠DCG = y°,则易得∠G = x° + y°,∠GEF = x° + 24°,∠GCF = y°。又因为易知∠HEF + ∠F + ∠FCD = 360°,∠HEF = 2x° + 24°,∠FCD = 2y°,所以 2x° + 24° + ∠F + 2y° = 360°。所以 2∠G + ∠F = 336°。所以∠G + $\frac{1}{2}$∠F = 168°。


查看更多完整答案,请扫码查看


