《2025年通城学典课时作业本七年级数学下册人教版》

17. 一个正数 x 的两个不同的平方根分别是 2a - 1 和 -a + 2. 化简：$2|a + \sqrt{2}| + |x - 2\sqrt{2}| - |3a + x|$.

答案： 由题意，得$(2a - 1)+(-a + 2)=0$，解得$a = -1$。$\therefore x=(2a - 1)^2=(-3)^2 = 9$。$\therefore$原式$=2\times|-1+\sqrt{2}|+|9 - 2\sqrt{2}|-|3\times(-1)+9|=2\sqrt{2}-2 + 9-2\sqrt{2}-6 = 1$

18. （2023·舟山）下列四个数中，比 1 小的正无理数是 （ ）
A. $\frac{\sqrt{6}}{3}$
B. $-\frac{\sqrt{3}}{3}$
C. $\frac{1}{3}$
D. $\frac{\pi}{3}$

答案： A

19. 文文设计了一个关于实数运算的程序，按此程序输入一个数后，输出的数比输入的数的平方小 1. 若输入 $\sqrt{7}$，则输出的数为 （ ）
A. 5
B. 6
C. 7
D. 8

答案： B

20. 在如图所示的数轴上，点 B 与点 C 关于点 A 对称，A，B 两点对应的实数分别是 $\sqrt{3}$ 和 -1，则点 C 对应的实数是 （ ）

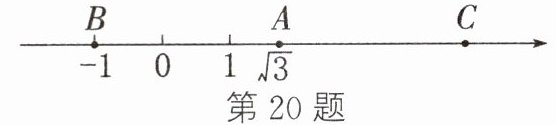
A. $1 + \sqrt{3}$
B. $2 + \sqrt{3}$
C. $2\sqrt{3} - 1$
D. $2\sqrt{3} + 1$

答案： D

21. 如果 m 是 2 024 的算术平方根，那么 $\frac{2 024}{100}$ 的平方根是 ________（用含 m 的式子表示）.

答案： $\pm\frac{m}{10}$

22. 大于 $-\sqrt{11}$ 而小于 $\sqrt{5}$ 的所有整数的和是 ________.

答案： -3

23. 小娟估算一个无理数的大小时，不慎将墨水瓶打翻，现只知道被开方数是 260，估算的结果在 6 和 7 之间，则根指数应为 ________.

答案： 3

24. 有一个正方体集装箱，容积为 64 $m^3$，现准备将其改造扩充，以便放置更多的货物，则其棱长增加 ________ m，才能使容积达到 512 $m^3$.

答案： 4

25. 对于任意两个不相等的实数 a，b，定义一种新运算：$a※b = \frac{\sqrt{a \cdot b}}{a - b}$. 例如：$3※2 = \frac{\sqrt{3×2}}{3 - 2}=\sqrt{6}$. 计算：$2※8 =$ ________.

答案： $-\frac{2}{3}$

26. 实数 a，b，c 在数轴上对应点的位置如图所示，化简：$|c| - \sqrt{(a + b)^2} + \sqrt{(b - c)^2} - \sqrt[3]{-b^3}$.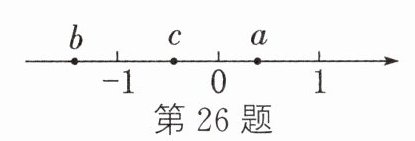

答案： 由数轴，可知$b ＜ -1 ＜ c ＜ 0 ＜ a ＜ 1$。$\therefore a + b ＜ 0$，$b - c ＜ 0$。$\therefore$原式$=-c+(a + b)-(b - c)+b=-c + a + b - b + c + b=a + b$