《2025年通城学典课时作业本七年级数学下册人教版》

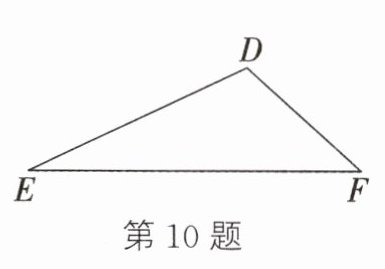
10. （教材P102探究2变式）如图所示为一块三角形土地，爷爷打算在这块三角形土地上种植$A$，$B$两种不同的花草，其中种植$A$种花草与种植$B$种花草的单位面积的费用之比为$2:3$. 这块三角形土地的一边$EF$的长为160 m，此边上的高为50 m，应怎样划分这块土地，才能使种植$A$，$B$两种花草的总费用的比为$2:5$？

答案： 方法不唯一，如设$G$是$EF$上一点，$GE = x$m，$FG = y$m。根据题意，得$\begin{cases}x + y = 160\\5(\frac{1}{2}x×50×2)=2(\frac{1}{2}y×50×3)\end{cases}$，解得$\begin{cases}x = 60\\y = 100\end{cases}$。$\therefore$在边$EF$上取一点$G$，使$GE = 60$m，连接$GD$，把三角形$DEF$分成两个三角形，在三角形$DEG$中种植A种花草，在三角形$DFG$中种植B种花草。

1. 某校七年级(2)班有40名同学为“希望工程”捐书，共捐了100本书. 捐书情况如下表：

表中捐2本书和3本书的人数不小心被墨水污染，已看不清楚. 设捐2本书的有$x$名同学，捐3本书的有$y$名同学. 根据题意，可列方程组为（ ）
A. $\begin{cases}x + y = 27, \\2x + 3y = 66\end{cases}$
B. $\begin{cases}x + y = 27, \\2x + 3y = 100\end{cases}$
C. $\begin{cases}x + y = 27, \\3x + 2y = 66\end{cases}$
D. $\begin{cases}x + y = 27, \\3x + 2y = 100\end{cases}$

答案： A

2. 某电视台组织知识竞赛，共设20道选择题，各题分值相同，每题必答，下表记录了2个参赛者的得分情况：

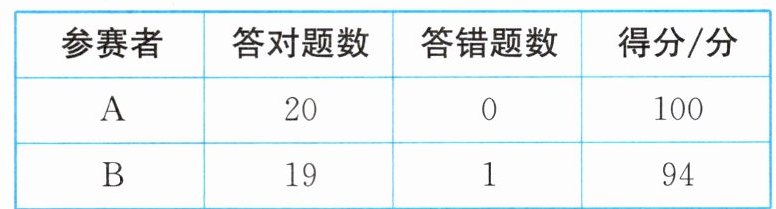
如果参赛者$C$的得分为76分，那么他答对了_______道题.

答案： 16

3. （教材P104练习第3题变式）小华从家到学校的路是一段平路和一段下坡路，假设他始终保持平路每分钟走60 m，下坡路每分钟走80 m，上坡路每分钟走40 m，则他从家到学校需10 min，从学校到家需15 min. 求小华家到学校的路程.

答案： 设小华家到学校的平路和下坡路分别有$x$m，$y$m。根据题意，得$\begin{cases}\frac{x}{60}+\frac{y}{80}=10\\\frac{x}{60}+\frac{y}{40}=15\end{cases}$，解得$\begin{cases}x = 300\\y = 400\end{cases}$。$\therefore300 + 400 = 700$（m）。答：小华家到学校的路程为700m。

4. 本地某快递公司规定：寄件不超过1千克的部分按起步价计费，寄件超过1千克的部分按千克计费. 小丽分别寄快递到上海和北京，收费标准及实际收费如下表：


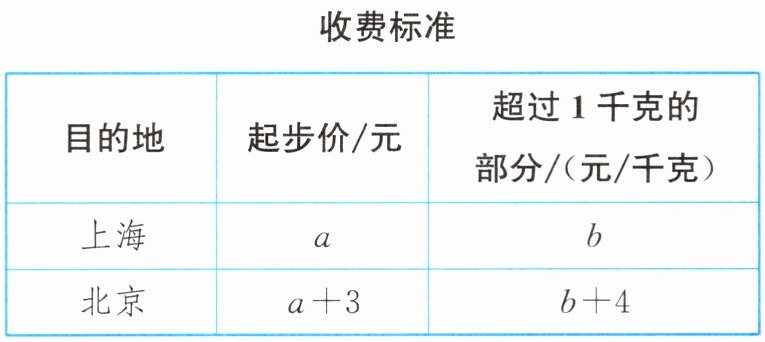
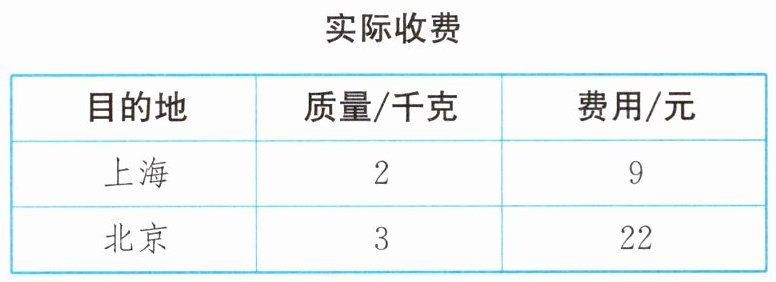
求$a$，$b$的值.

答案： 依题意，得$\begin{cases}a+(2 - 1)b = 9\\a + 3+(3 - 1)(b + 4)=22\end{cases}$，解得$\begin{cases}a = 7\\b = 2\end{cases}$。

5. 一辆汽车从$A$地出发，向东行驶，途中要经过$B$地. 在规定的某一时间内，若车速为60 km/h，则能驶过$B$地2 km；若车速为50 km/h，则还差3 km才能到达$B$地. 设$A$，$B$两地间的路程为$x$ km，规定时间为$y$ h，可列出的方程组是（ ）
A. $\begin{cases}60y - x = 2, \\x = 3 + 50y\end{cases}$
B. $\begin{cases}60y - x = 2, \\50y - x = 3\end{cases}$
C. $\begin{cases}60y = x - 2, \\50y = x - 3\end{cases}$
D. $\begin{cases}60y = x - 2, \\50y = x + 3\end{cases}$

答案： A

6. 足球比赛的记分规则是胜一场记3分，平一场记1分，负一场记0分. 一支足球队参加了15场比赛，负了4场，共得29分，则这支球队胜了（ ）
A. 5场
B. 7场
C. 9场
D. 11场

答案： C

7. 一批机器零件共840个，若甲先做4天，然后乙加入一起做，则再做8天才能完成；若乙先做4天，然后甲加入一起做，则再做9天才能完成. 甲每天做_______个零件，乙每天做_______个零件.

答案： 50 30

8. 某种植户计划安排10个劳动力同时耕种30亩土地（亩：中国市制土地面积单位），这些土地可以种蔬菜，也可以种水稻，种植这些作物所需的劳动力及预计产值如下表：

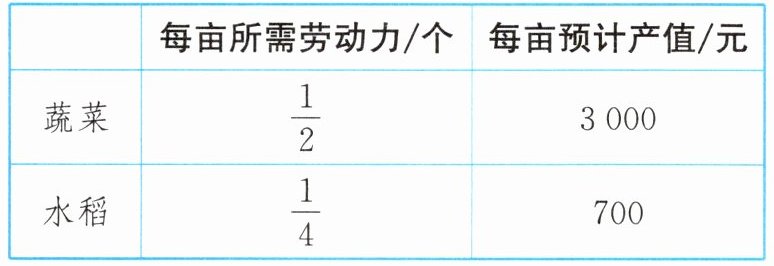
为了使所有的土地种上作物，全部劳动力都有工作，则应安排种植蔬菜的劳动力为_______个，这时预计总产值为_______元.

答案： 5 44000

9. （教材P104练习第2题变式）“五一”期间，桂林秀甲天下的自然风光和人头攒动的热闹景象“霸屏”央视. 据统计，全市共接待游客482.35万人次，实现旅游总收入50.16亿元. 某外地游客购买了三种桂林特色商品，因不小心污染了商品销售单上的部分信息，导致部分信息无法识别，根据下表解决问题：

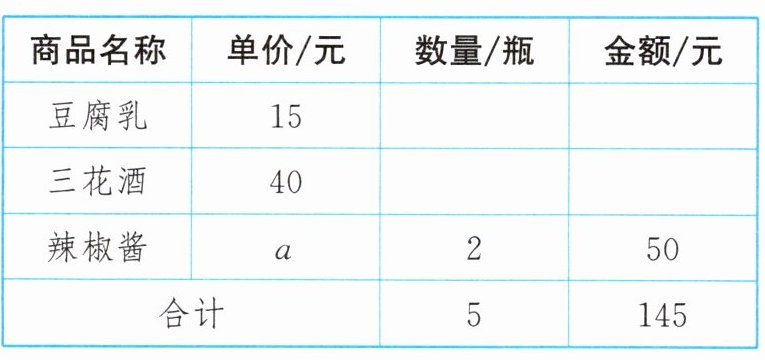
（1）某游客购买豆腐乳、三花酒各几瓶？
（2）某游客再次购买3瓶豆腐乳、4瓶三花酒和3瓶辣椒酱共花多少钱？

答案： （1）设游客购买豆腐乳$x$瓶、三花酒$y$瓶。根据题意，得$\begin{cases}x + y = 5 - 2\\15x + 40y = 145 - 50\end{cases}$，解得$\begin{cases}x = 1\\y = 2\end{cases}$。答：游客购买豆腐乳1瓶、三花酒2瓶。（2）$a = 50÷2 = 25$，$3×15 + 4×40 + 3×25 = 280$（元）。答：购买3瓶豆腐乳、4瓶三花酒和3瓶辣椒酱共花280元。

10. 北京、上海两地的两个厂家同时生产同种型号的大型计算机，除本地使用外，北京可调运给外地10台，上海可调运给外地4台，现协议调运给武汉6台、重庆8台，每台的运费如下表：

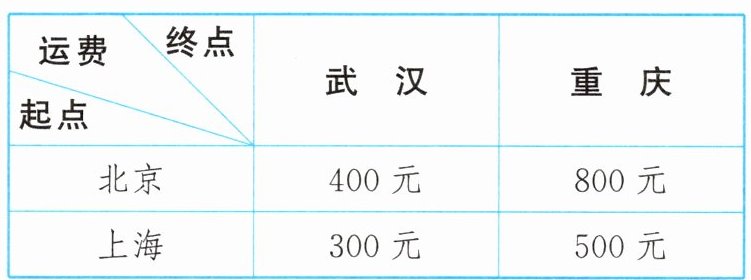
现有一种调运方案，运费是7600元，则在这种调运方案中，北京、上海应分别调运给武汉、重庆各几台大型计算机？

答案： 设北京调运给武汉$x$台大型计算机，调运给重庆$y$台大型计算机，则上海调运给武汉$(6 - x)$台大型计算机，调运给重庆$(8 - y)$台大型计算机。根据题意，得$\begin{cases}x + y = 10\\400x + 800y + 300(6 - x)+500(8 - y)=7600\end{cases}$，解得$\begin{cases}x = 6\\y = 4\end{cases}$。$\therefore6 - x = 0$，$8 - y = 4$。答：在这种调运方案中，北京调运给武汉6台大型计算机，调运给重庆4台大型计算机；上海调运给武汉0台大型计算机，调运给重庆4台大型计算机。