《2025年经纶学典提高班六年级数学下册苏教版》

1. 将体积相同的水倒入底面积不同的杯子里。根据表中的数据，回答问题。
　　
　　(1)表中，(　　　　　　　)和(　　　　　　　　)是两种相关联的量。(　　　　　　　)随着(　　　　　　　　)的变化而变化。
　　(2)写出3组这两个量对应的两个数的积，并比较积的大小。
　　(3)上面所求乘积的意义是(　　　　　　　　)。
　　(4)表中相关联的两种量成反比例吗？为什么？

答案：
(1)水的高度 杯子的底面积 水的高度 杯子的底面积
(2)$30×10 = 300$ $20×15 = 300$ $15×20 = 300$ $300 = 300 = 300$(合理即可)
(3)水的体积
(4)成反比例，因为水的高度和杯子的底面积的乘积是一定的。(合理即可)

2. 填空题。
　　(1)单价×数量=(　　　)，当(　　　)一定时，(　　　)和(　　　)成反比例。
　　(2)工作效率×工作时间=(　　　　　)，当(　　　　　)一定时，(　　　　　)和(　　　　　)成反比例。
　　(3)用x和y表示两种相关联的量，用k(一定)表示它们的乘积，反比例关系用式子(　　　　　)表示。

答案：
(1)总价 总价 单价 数量
(2)工作总量 工作总量 工作效率 工作时间
(3)$x×y = k$

3. 判断下面各题中的两种量是否成反比例，是的在括号里画“√”，不是的画“×”。
　　(1)非零自然数和它的倒数。　　　　(　　　)
　　(2)20÷a=b(a不等于0)，a和b。　　　(　　　)
　　(3)订阅《小学生数学报》的份数和总钱数。　　　　　　　　　　　　　　　(　　　)
　　(4)被减数一定，减数和差。　　　　　(　　　)
　　(5)时间一定时，印刷报纸的速度与印刷报纸的总张数。　　　　　　　　　　　　(　　　)
　　(6)铺地面积一定时，每块地砖的面积和铺地砖的块数。　　　　　　　　　　　　(　　　)

答案：
(1)√
(2)√
(3)×
(4)×
(5)×
(6)√

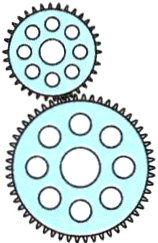
4. 新情境 生活百科 机械手表中不同的齿轮以不同的速度旋转，驱动指针显示时间。如图，大齿轮的齿数是54，小齿轮的齿数是36。
　　(1)旋转时大齿轮和小齿轮相互咬合的齿数是一定的。齿数和转过的圈数成(　　　)比例。
　　(2)大齿轮旋转2周时，小齿轮需要旋转(　　　)周。
　　

答案：
(1)反
(2)3

5. 已知6÷a=$\frac{1}{6}$×b(a、b均不为0)，则a和b成什么比例关系？为什么？

答案： 成反比例关系，因为$6÷a=\frac{1}{6}×b$，$ab = 36$，乘积一定，所以成反比例关系。(合理即可)
提示：因为$6÷a=\frac{1}{6}×b$，即$\frac{6}{a}=\frac{b}{6}$，根据比例的基本性质，可得$a×b = 6×6 = 36$，即$a$和$b$的乘积一定，所以$a$和$b$成反比例关系。

6. 一艘巡逻艇所带的柴油最多可以用8小时，驶出时顺风，每小时行90千米；驶回时逆风，每小时行驶的路程是顺风时的$\frac{4}{5}$，这艘巡逻艇最多驶出多远就应该往回行驶？

答案： $8×\frac{4}{5 + 4}×90 = 320$(千米)
答：最多驶出320千米就应该往回行驶。
提示：行驶路程相同，$v_{顺}:v_{逆}=5:4$，$t_{顺}:t_{逆}=4:5$，$8×\frac{4}{5 + 4}×90 = 320$(千米)。