《2025年经纶学典提高班六年级数学下册苏教版》

1. 填空题。
(1)一个圆柱和一个圆锥等底等高，它们的体积之和为240立方分米，那么圆柱的体积是(　　　)立方分米，圆锥的体积是(　　　)立方分米。
(2)如图，有一个直角三角形，分别绕它的两条直角边所在的直线旋转一周，可以形成两个圆锥，这两个圆锥的体积相差(　　　)立方厘米。

答案： 1.
(1)180　60　
(2)50.24

2. 选择题。
(1)一个圆柱和一个圆锥的底面直径相等，圆锥的高是圆柱的3倍，圆锥的体积是12立方厘米，则圆柱的体积是(　　　)立方厘米。
A. 4 B. 6 C. 12 D. 36
(2)一个圆锥的底面直径和高都扩大到原来的3倍，它的体积就扩大到原来的(　　　)倍。
A. 3 B. 9 C. 18 D. 27
(3)将一个圆锥在$\frac{1}{2}$高度处拦腰切开，则上、下两部分的体积之比为(　　　)。
A. 1 : 3 B. 1 : 4 C. 1 : 8 D. 1 : 7

答案： 2.
(1)C　
(2)D　
(3)D

3. 建筑工人使用一种圆锥形铜锤，底面半径是2厘米，高是6厘米。如果每立方厘米铜重8.9克，那么这个铜锤约重多少克？(结果保留两位小数)

答案： $\frac{1}{3} \times 3.14 \times 2^{2} \times 6 = 25.12$（立方厘米） 25.12×8.9≈223.57（克） 答：这个铜锤约重223.57克。

4. 新情境 数学文化《九章算术》是我国古代内容极为丰富的数学名著。该书中有如下问题：“今有委米依垣内角，下周八尺，高五尺。问：积及委米几何？”王老师出了一道类似的题目考考大家：在屋内墙角处堆放米(如图，米堆为一个圆锥的四分之一)，米堆底部的弧长为6尺，米堆的高为4尺，问米堆的体积和堆放的米各为多少？已知1斛米的体积约为1.6立方尺，圆周率约为3，估算堆放的米约有多少斛。

答案： 6×4÷3÷2 = 4(尺)$\frac{1}{4} \times \frac{1}{3} \times 3 \times 4^{2} \times 4 = 16$(立方尺)16÷1.6 = 10(斛)答：米堆的体积是16立方尺，堆放的米约有10斛。

5. 一个圆柱和一个圆锥的高相等，体积比是3 : 2，如果圆柱的底面积是9.42平方厘米，那么圆锥的底面积是多少？如果圆锥的底面积是9.42平方厘米，那么圆柱的底面积是多少？

答案： 圆锥：9.42×2 = 18.84(平方厘米)圆柱：9.42÷2 = 4.71(平方厘米)答：圆锥的底面积是18.84平方厘米，圆柱的底面积是4.71平方厘米。提示：一个圆柱和一个圆锥的高相等，体积比是3:2，那么它们的底面积之比是1:2，根据这个关系即可求解。

6. 圆台是由一个圆锥截去上面部分得到的，如图。已知这个圆台截去的圆锥的高也是15厘米，求这个圆台的体积。

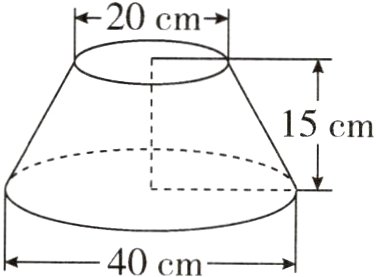
答案： $\frac{1}{3} \times 3.14 \times (40 \div 2)^{2} \times (15 + 15) - \frac{1}{3} \times 3.14 \times (20 \div 2)^{2} \times 15 = 10990$(立方厘米)答：这个圆台的体积是10990立方厘米。提示：圆台的体积等于原来圆锥的体积减去截去的圆锥的体积。