《2025年经纶学典提高班六年级数学下册苏教版》

1.学校里建了一个圆柱形水池，如图。
(1)小轩想知道水池里水的质量，需要用到的数据有( )。(填序号)
①水池内底面直径是4米。 ②水池内底面周长是12.56米。
③水池深1.5米。 ④水池的池沿宽0.5米。
⑤水池里水深1.2米。 ⑥1立方米水的质量是1吨。

(2)根据你选择的数据，计算水池里水的质量。

答案：
(1)①⑤⑥(答案不唯一)
(2)3.14×(4÷2)²×1.2×1 = 15.072(吨)
答：水池里水的质量是15.072吨。

2.新趋势 评价说明 下面是小玲错题本上的一道题，请你分析一下她错误的原因，并正确解答。

错误原因：
正确解答：

答案： 错误原因：误把圆柱形零件的高当作圆柱浸入水中的长度来计算。
正确解答：3.14×3²×5×2 = 282.6(立方厘米)
答：从容器中溢出的水的体积是282.6立方厘米。

3.新趋势 推导探究 如图，小凯和小兰在探究直角梯形绕上底和下底所在直线旋转一周后得到的图形，图中直角梯形下底的长度是上底长度的2倍。

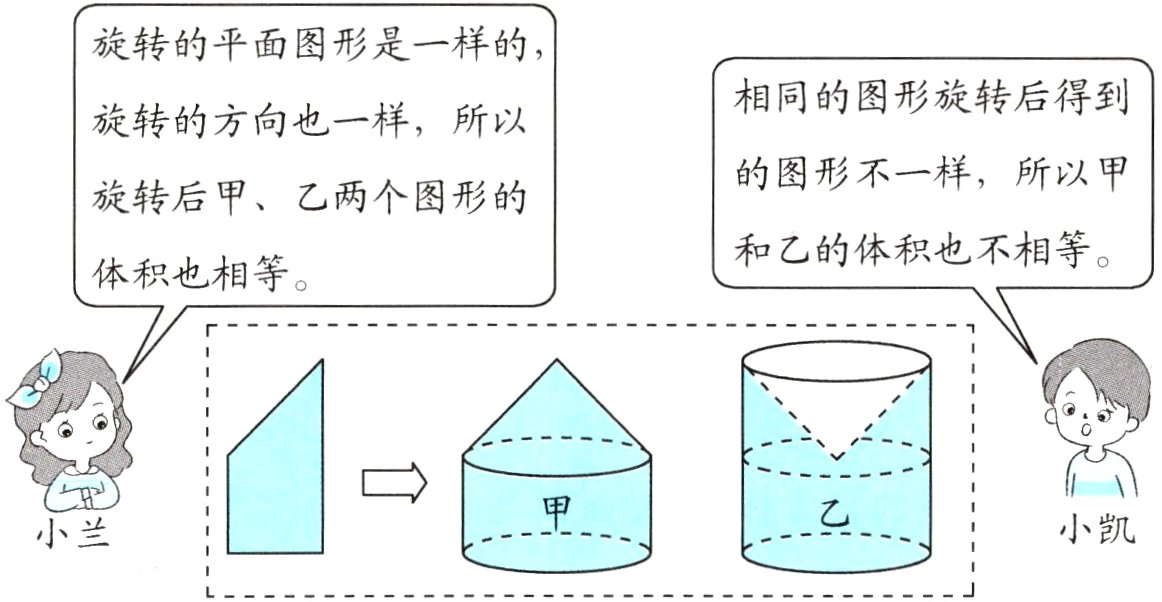
(1)你同意谁的说法？ ( )
(2)甲、乙两个立体图形的表面积( )。(填"相等"或"不相等")
(3)求甲、乙两个立体图形的体积之比。

答案：
(1)小凯
(2)不相等
(3)$(1 + \frac{1}{3}):(2 - \frac{1}{3}) = 4:5$
答：甲、乙两个立体图形的体积之比是4:5。
提示：乙上半部分可以看作从圆柱上挖去一个等底等高的圆锥，该圆锥的体积是上半部分圆柱体积的$\frac{1}{3}$，所以剩余部分是圆锥体积的2倍，因此甲、乙两个立体图形的体积不相等，体积之比根据等底等高的圆柱与圆锥的体积比可直接写出，然后化简即可。