《2025年经纶学典提高班六年级数学下册苏教版》

1. 填空题。
　(1) 一个圆锥的底面半径是2厘米，高是3厘米，这个圆锥的占地面积是(　　　)平方厘米，体积是(　　　)立方厘米。
　(2) 一个圆柱和一个圆锥等底等高，如果圆柱的体积是15立方分米，那么圆锥的体积是(　　　)立方分米；如果圆锥的体积是15立方分米，那么圆柱的体积是(　　　)立方分米。
　(3) 一个圆柱和一个圆锥等底等高，体积相差18立方厘米。圆柱的体积是(　　　)立方厘米，圆锥的体积是(　　　)立方厘米。

答案： 1.
(1)12.56 12.56
(2)5 45
(3)27 9

2. 选择题。
　(1) 将一个圆柱削成一个最大的圆锥，削去部分的体积是圆锥体积的(　　　)，削去部分的体积是圆柱体积的(　　　)。
　A. $\frac{1}{2}$　　　B. $\frac{1}{3}$　　　C. $\frac{2}{3}$　　　D. 2倍
　(2) 一个直角三角形，两条直角边分别是6分米和8分米，如果以其中的一条较长的直角边所在直线为轴旋转一周，得到圆锥的体积是(　　　)立方分米。
　A. 75.36　B. 100.48　C. 301.44　D. 401.92

答案： 2.
(1)D C
(2)C

3. 计算下面各圆锥的体积。(单位：厘米)
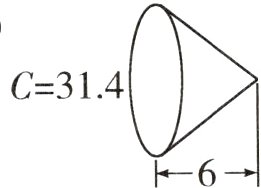
　(1)
　(2)

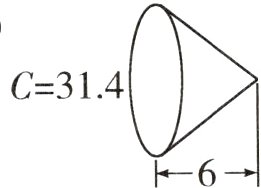
答案： 3.
(1)$3.14\times(6\div2)^{2}\times6\times\frac{1}{3}=56.52$(立方厘米)
(2)$31.4\div3.14\div2 = 5$(厘米)
$3.14\times5^{2}\times6\times\frac{1}{3}=157$(立方厘米)

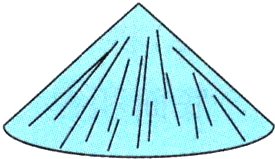
4. 新趋势 学科融合 “青箬笠，绿蓑衣，斜风细雨不须归”描述了渔翁乐然垂钓的场景。如图是一种箬笠，它近似于圆锥，底面直径是40厘米，高是24厘米，把它扣在地上，所占空间是多少立方厘米？(厚度忽略不计)
　

答案： 4. $40\div2 = 20$(厘米)
$3.14\times20^{2}\times24\times\frac{1}{3}=10048$(立方厘米)
答：所占空间是10048立方厘米。

5. (名校期末真题)把一个底面半径是3厘米、高是12厘米的圆锥形容器装满水，再倒入底面半径是2厘米、高是10厘米的圆柱形容器中。圆柱形容器能完全装下吗？如果装得下，请求出圆柱形容器中水面的高度；如果装不下，请求出溢出水的体积。(容器壁厚度忽略不计)

答案： 5. $\frac{1}{3}\times3.14\times3^{2}\times12 = 113.04$(立方厘米)
$113.04\div3.14\div2^{2}=9$(厘米) $9＜10$
答：圆柱形容器能完全装下，圆柱形容器中水面的高度是9厘米。

6. 把一个高8厘米的圆锥沿着高对半切开，增加的表面积为72平方厘米，求这个圆锥的底面积和体积。

答案： 6. $72\div2\times2\div8 = 9$(厘米)
$3.14\times(9\div2)^{2}=63.585$(平方厘米)
$63.585\times8\times\frac{1}{3}=169.56$(立方厘米)
答：这个圆锥的底面积是63.585平方厘米，体积是169.56立方厘米。
提示：增加的表面积是切面为两个等腰三角形的面积和，等腰三角形的高就是圆锥的高，等腰三角形的底边是圆锥的底面直径。

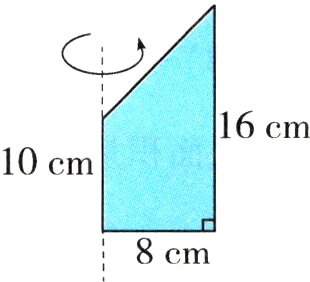
7. 如图，一个直角梯形的上底是10厘米，下底是16厘米，高是8厘米，用上底所在直线作轴旋转一周。求所得到的立体图形的体积。
　　　　　　　　　　　

答案： 7. $3.14\times8^{2}\times16-\frac{1}{3}\times3.14\times8^{2}\times(16 - 10)=2813.44$(立方厘米)
答：所得到的立体图形的体积是2813.44立方厘米。
提示：该立体图形为底面半径是8厘米、高是16厘米的圆柱挖去一个底面半径是8厘米、高是(16 - 10)厘米的圆锥，代入体积公式计算即可。