《2025年经纶学典提高班六年级数学下册苏教版》

1. 填空题。
　　(1)挖一个底面半径是4米的圆柱形蓄水池，要使蓄水池能蓄水62.8立方米，这个蓄水池要挖(　　　)米深。
　　(2)一个长方形的长是6厘米，宽是2厘米，以它的长所在直线为轴旋转一周所得到的圆柱的体积是(　　　)立方厘米。
　　(3)把一个圆柱沿着底面直径切开，得到一个长是10厘米、宽是4厘米的长方形截面，这个圆柱的体积是(　　　)立方厘米或(　　　)立方厘米。
　　(4)一根圆柱形木头长2米，若截成相同的3段小圆柱后，表面积增加了100平方分米，原来这根木头的底面积是(　　　)平方分米，体积是(　　　)立方分米。

答案： 1.
(1) 1.25
(2) 75.36
(3) 125.6 314
(4) 25 500

2. 选择题。
　　(1)一个圆柱，高扩大为原来的2倍，底面直径缩小为原来的$\frac{1}{2}$，体积(　　　)。
　　A. 不变
　　B. 扩大到原来的2倍
　　C. 缩小为原来的$\frac{1}{2}$
　　D. 缩小为原来的$\frac{1}{4}$
　　(2)圆柱、正方体和长方体的底面周长、高分别相等，则它们的体积相比，(　　　)。
　　A. 圆柱最大
　　B. 正方体最大
　　C. 长方体最大
　　D. 一样大

答案： 2.
(1)C
(2)A

3. 一个圆柱形水池，水池底面直径为8米，池深1.8米。这个水池最多能盛水多少升?

答案： 3. $3.14\times(8\div2)^2\times1.8 = 90.432$（立方米）
90.432立方米 = 90432升
答：这个水池最多能盛水90432升。

4. 王老师家有一个长方体鱼缸，长、宽、高分别为6分米、3.5分米、2.5分米，鱼缸内水深2分米，鱼缸内的假山浸没在水中，体积为5立方分米。换水时，把鱼缸里的水倒入一个圆柱形水桶内，已知从里面量，水桶的底面积为10平方分米，高是4分米。这个水桶能装下这些水吗？

答案： 4. $6\times3.5\times2 - 5 = 37$（立方分米）
$10\times4 = 40$（立方分米） $40＞37$
答：这个水桶能装下这些水。

5. 新情境 人文历史 已知一种圆形钱币(如图)直径约为8厘米，厚度为4毫米，正中间的正方形缺口边长为2厘米。如果把20个这样的钱币对齐正方形缺口垒起来，垒起来的钱币的体积大约是多少立方厘米?
　

答案： 5. 4毫米 = 0.4厘米 $3.14\times(8\div2)^2\times0.4\times20 - 2\times2\times0.4\times20 = 369.92$（立方厘米）
答：垒起来的钱币的体积大约是369.92立方厘米。
提示：由题图可知，20个这样的钱币垒起来就是一个圆柱，垒起来的体积 = 圆柱的体积 - 内部长方体的体积，根据圆柱的体积 = $\pi r^{2}h$，长方体的体积 = 长×宽×高，代入数据解答即可。

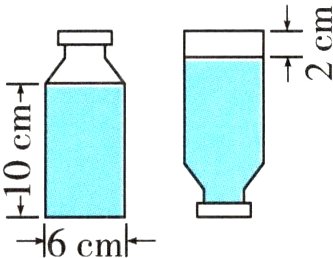
6. 如图是一个饮料瓶，瓶中装有一些饮料。这个饮料瓶的容积是多少毫升？
　　　　　　　　　　　

答案： 6. $3.14\times(6\div2)^2\times(10 + 2)=339.12$（立方厘米）
339.12立方厘米 = 339.12毫升
答：这个饮料瓶的容积是339.12毫升。
提示：瓶子里饮料倒放后体积不变，饮料的体积加上2厘米高的圆柱的体积就是饮料瓶的容积。