《2025年全品学练考九年级数学下册华师大版》

模块7 圆中的计算问题
（1）如果弧长为l，圆心角的度数为n，圆的半径为r，那么弧长的计算公式为______；
（2）如果扇形面积为S，弧长为l，圆心角的度数为n，圆的半径为r，那么扇形面积的计算公式为______．

答案：
(1)$l=\frac{n\pi r}{180}$　
(2)$S=\frac{n\pi r^{2}}{360}$或$S=\frac{1}{2}lr$

例7 如图27 - T - 6，在矩形ABCD中，AB = 2，BC = 4，E为BC的中点，连结AE，DE，以E为圆心，EB长为半径画弧，分别与AE，DE交于点M，N，则图中阴影部分的面积为______．（结果保留π）

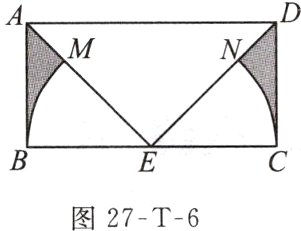
答案： 4 - π

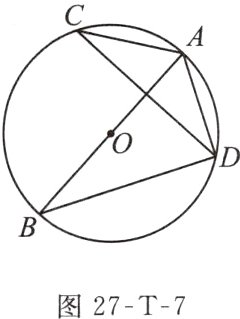
例8 如图27 - T - 7，AB是⊙O的直径，点C，D均在⊙O上，∠ACD = 30°，弦AD = 4 cm．
（1）求⊙O的直径；
（2）求$\overset{\frown}{AD}$的长．

答案：
(1)8 cm　
(2)$\frac{4\pi}{3}$ cm

模块8 正多边形与圆
（1）正多边形与圆的关系：任何正多边形都有一个______和一个______．
（2）正多边形的有关概念：
正多边形的中心：正多边形的______（或内切圆）的圆心叫做正多边形的中心．
正多边形的半径：外接圆的______叫做正多边形的半径．
正多边形的边心距：______的半径叫做正多边形的边心距．
正多边形的中心角：正多边形每一条边所对的外接圆的圆心角都相等，叫做正多边形的中心角．正n（n≥3，且n为整数）边形的每个中心角都等于______．

答案：
(1)外接圆　内切圆
(2)外接圆　半径　内切圆　$\frac{360^{\circ}}{n}$

例9 如图27 - T - 8，已知正六边形ABCDEF的周长为24 cm，求这个正六边形的半径R，边心距r，中心角α和面积S．

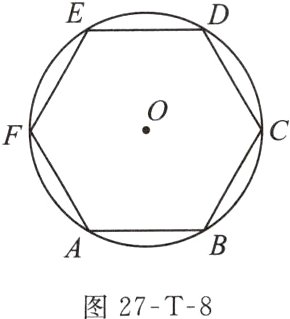
答案： 解:过点O作OM⊥AB于点M，连结OA，OB，则OA = OB，AM = BM.
∵正六边形ABCDEF的周长为24 cm，
∴AB = 4 cm，α = ∠AOB = 360°÷6 = 60°，则△OAB是等边三角形，AM = BM = 2 cm，
∴R = OA = OB = AB = 4 cm.则$r = OM=\sqrt{AO^{2}-AM^{2}}=\sqrt{4^{2}-2^{2}} = 2\sqrt{3}$(cm)，
∴$S = 6S_{\triangle OAB}=6\times\frac{1}{2}AB\cdot OM = 6\times\frac{1}{2}\times4\times2\sqrt{3}=24\sqrt{3}$(cm²).

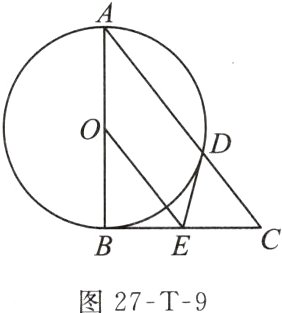
例10 如图27 - T - 9，以Rt△ABC的直角边AB为直径作⊙O，交斜边AC于点D，E是BC的中点，连结OE，DE．
（1）求证：DE是⊙O的切线；
（2）若sinC = $\frac{4}{5}$，DE = 5，求AD的长．

答案：
解:
(1)证明:如图，连结BD，OD.
∵AB是⊙O的直径，
∴∠ADB = 90°，即BD⊥AC.在Rt△BDC中，
∵E是BC的中点，
∴$BE = DE=\frac{1}{2}BC$.又
∵OB = OD，OE = OE，
∴△OBE≌△ODE，
∴∠OBE = ∠ODE = 90°.又
∵OD是⊙O的半径，
∴DE是⊙O的切线.
(2)由
(1)中结论，得BC = 2DE = 10.在Rt△BDC中，$\sin C=\frac{BD}{BC}=\frac{BD}{10}=\frac{4}{5}$，
∴BD = 8，
∴$CD=\sqrt{BC^{2}-BD^{2}} = 6$.
∵∠A + ∠C = 90°，∠A + ∠ABD = 90°，
∴∠C = ∠ABD.又
∵∠ADB = ∠BDC = 90°，
∴△ADB∽△BDC，
∴$\frac{AD}{BD}=\frac{BD}{CD}$，
∴$AD=\frac{BD^{2}}{CD}=\frac{8^{2}}{6}=\frac{32}{3}$.