《2025年全品学练考九年级数学下册华师大版》

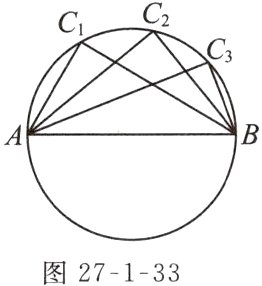
1. 如图27 - 1 - 33，在圆中，圆周角∠AC₁B = ∠AC₂B = ∠AC₃B = 90°，那么弦AB一定是直径吗？你能用反证法加以证明吗？

答案：
解：弦AB一定是直径.
证明：如图，假设AB不是圆的直径，不妨设AD是圆的一条直径，连结C₁D. 则∠AC₁D=90°.
∵∠AC₁B = 90°，且由图可知，∠AC₁B≠∠AC₁D，
∴假设不成立，
∴弦AB一定是直径.

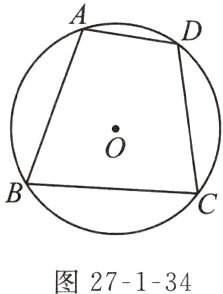
2. 如图27 - 1 - 34，四边形ABCD的四个顶点都在⊙O上，那么这个四边形的对角之间有什么关系呢？并加以证明.

答案：
解：对角互补.
证明：如图，连结OB，OD.
∵∠1 = 2∠C，∠2 = 2∠A，∠1+∠2=360°，
∴2∠A+2∠C=360°，
即∠A+∠C=180°.
∵∠A+∠ABC+∠C+∠ADC=360°，
∴∠ABC+∠ADC=180°.
∴这个四边形的对角互补.

[概括新知]
圆周角定理的推论：
推论1：90°的圆周角所对的弦是__________.
如果一个圆经过一个多边形的各个顶点，这个圆就叫做这个多边形的__________，这个多边形叫做这个圆的__________.
推论2：圆内接四边形的对角__________.

答案： 直径 外接圆 内接多边形 互补

例4 如图27 - 1 - 35，四边形ABCD为⊙O的内接四边形，若四边形OBCD为菱形，则∠A的度数为（ ）

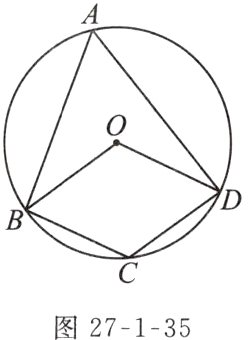
A.45°
B.60°
C.72°
D.36°

答案： B

例5 如图27 - 1 - 36，四边形ABCD内接于⊙O，E是CB的延长线上一点，∠EBA = 125°，则∠D的度数为（ ）

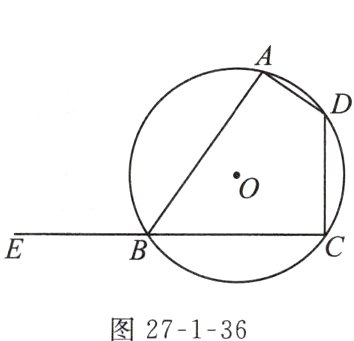
A.65°
B.120°
C.125°
D.130°

答案： C