搜索
解答下列问题:
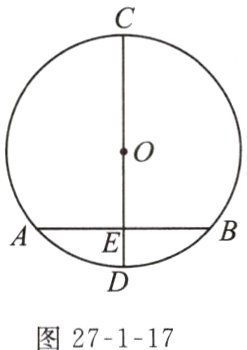
问题1:如图27−1−17，AB是⊙O的一条弦，E是线段AB的中点，作直线OE 交⊙O于点C，D.
(1)CD⊥AB吗？为什么？
(2)$\overset{\frown}{AC}$与$\overset{\frown}{BC}$相等吗？$\overset{\frown}{AD}$与$\overset{\frown}{BD}$相等吗？
问题1:如图27−1−17，AB是⊙O的一条弦，E是线段AB的中点，作直线OE 交⊙O于点C，D.
(1)CD⊥AB吗？为什么？
(2)$\overset{\frown}{AC}$与$\overset{\frown}{BC}$相等吗？$\overset{\frown}{AD}$与$\overset{\frown}{BD}$相等吗？
答案：
问题1:解:
(1)$CD\perp AB$.
理由:如图，连结 $AO$，$BO$，则 $AO = BO$.
又 $AE = BE$，$\therefore CD\perp AB$.
(2)由垂径定理可得$\overset{\frown}{AC}=\overset{\frown}{BC}$，$\overset{\frown}{AD}=\overset{\frown}{BD}$.
问题1:解:
(1)$CD\perp AB$.
理由:如图，连结 $AO$，$BO$，则 $AO = BO$.
又 $AE = BE$，$\therefore CD\perp AB$.(2)由垂径定理可得$\overset{\frown}{AC}=\overset{\frown}{BC}$，$\overset{\frown}{AD}=\overset{\frown}{BD}$.
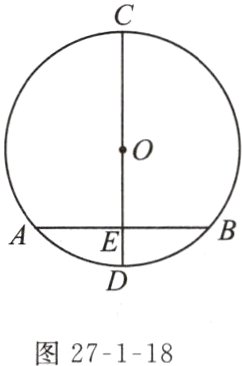
问题2:如图27−1−18，AB是⊙O的一条弦，D为$\overset{\frown}{AB}$的中点，作直线OD交AB于点E，交⊙O于点C.
(1)CD⊥AB吗？请说明理由;
(2)AE=BE吗？请说明理由.
(1)CD⊥AB吗？请说明理由;
(2)AE=BE吗？请说明理由.
答案：
问题2:解:
(1)$CD\perp AB$.
理由:连结 $OA$，$OB$.
$\because D$为$\overset{\frown}{AB}$的中点，$\therefore \overset{\frown}{AD}=\overset{\frown}{BD}$，
$\therefore \angle AOD=\angle BOD$，即 $OD$平分$\angle AOB$.
又$\because OA = OB$，$\therefore OD\perp AB$，即 $CD\perp AB$.
(2)$AE = BE$.理由:由
(1)知 $OA = OB$，$OD\perp AB$，$\therefore AE = BE$.
(1)$CD\perp AB$.
理由:连结 $OA$，$OB$.
$\because D$为$\overset{\frown}{AB}$的中点，$\therefore \overset{\frown}{AD}=\overset{\frown}{BD}$，
$\therefore \angle AOD=\angle BOD$，即 $OD$平分$\angle AOB$.
又$\because OA = OB$，$\therefore OD\perp AB$，即 $CD\perp AB$.
(2)$AE = BE$.理由:由
(1)知 $OA = OB$，$OD\perp AB$，$\therefore AE = BE$.
垂径定理的推论:平分弦(不是直径)的直径______________,并且____________;平分弧的直径垂直平分这条弧所对的弦.
答案：
垂直于这条弦 平分这条弦所对的两条弧
例2 如图27−1−19，⊙O的直径CD=10，AB是⊙O的弦，AB⊥CD，垂足为M，OM=3，求AB的长.
答案：
8
查看更多完整答案，请扫码查看
