1. 如图27 - 2 - 24,$P$为$\odot O$外一点,$PA$切$\odot O$于点$A$.若$PA = 3$,$\angle APO = 45^{\circ}$,则$\odot O$的半径是______.
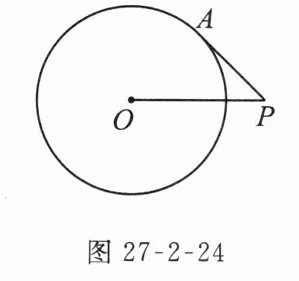

答案:
3
2. 如图27 - 2 - 25,$AB$为$\odot O$的弦,$AC$切$\odot O$于点$A$,$BC$过圆心$O$.若$\angle B = 20^{\circ}$,则$\angle C =$______$^{\circ}$.
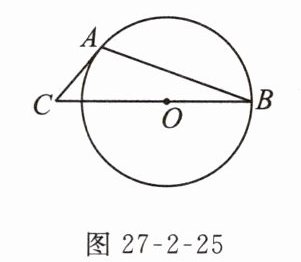

答案:
50
3. 如图27 - 2 - 26,直线$AB$经过$\odot O$上的点$C$,并且$OA = OB$,$CA = CB$.
求证:直线$AB$是$\odot O$的切线.
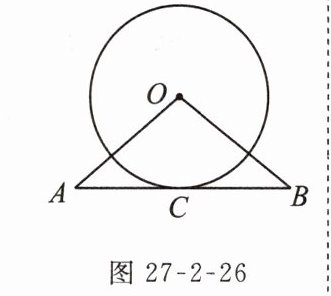
求证:直线$AB$是$\odot O$的切线.

答案:
证明:连结 OC,如图.
∵OA = OB,CA = CB,
∴OC⊥AB.
又
∵点 C 在⊙O 上,
∴直线 AB 是⊙O 的切线.

证明:连结 OC,如图.
∵OA = OB,CA = CB,
∴OC⊥AB.
又
∵点 C 在⊙O 上,
∴直线 AB 是⊙O 的切线.

4. 如图27 - 2 - 27,$AB$是$\odot O$的直径,$C$是$\odot O$上一点,过点$C$作$\odot O$的切线$CD$,交$AB$的延长线于点$D$,过点$A$作$AE\perp CD$,交$DC$的延长线于点$E$.
(1)若$\angle EAC = 25^{\circ}$,求$\angle ACD$的度数;
(2)若$OB = 2$,$BD = 1$,求$CE$的长.
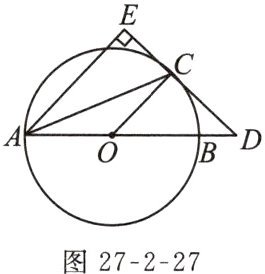
(1)若$\angle EAC = 25^{\circ}$,求$\angle ACD$的度数;
(2)若$OB = 2$,$BD = 1$,求$CE$的长.

答案:
(1)115°
(2)$\frac{2}{3}\sqrt{5}$
(1)115°
(2)$\frac{2}{3}\sqrt{5}$
如图27 - 2 - 28,已知PA,PB为⊙O的两条切线,A,B为切点,把⊙O沿着直线OP对折,你能发现什么?请证明你所发现的结论.


答案:
发现:PA=PB,∠APO=∠BPO.
证明:连结OA,OB,如图.

∵PA切⊙O于点A,
∴OA⊥PA.
同理可得OB⊥PB.
在Rt△OAP和Rt△OBP中,
∵OA=OB,OP=OP,
∴Rt△OAP≌Rt△OBP,
∴PA=PB,∠APO=∠BPO.
发现:PA=PB,∠APO=∠BPO.
证明:连结OA,OB,如图.

∵PA切⊙O于点A,
∴OA⊥PA.
同理可得OB⊥PB.
在Rt△OAP和Rt△OBP中,
∵OA=OB,OP=OP,
∴Rt△OAP≌Rt△OBP,
∴PA=PB,∠APO=∠BPO.
切线长及切线长定理:
(1)圆的切线上某一点与__________之间的线段的长叫做这点到圆的切线长.
(2)过圆外一点所画的圆的两条切线,____________________相等.这一点和圆心的连线平分______________________.
(1)圆的切线上某一点与__________之间的线段的长叫做这点到圆的切线长.
(2)过圆外一点所画的圆的两条切线,____________________相等.这一点和圆心的连线平分______________________.
答案:
(1)切点
(2)它们的切线长 这两条切线的夹角
(1)切点
(2)它们的切线长 这两条切线的夹角
查看更多完整答案,请扫码查看


