(1)由组成圆心角的两条________和圆心角所对的________围成的图形叫做扇形.
(2)圆心角为n°,半径为r,弧长为l的扇形的面积的计算公式是$S_{扇形}=__________ = __________. $
(2)圆心角为n°,半径为r,弧长为l的扇形的面积的计算公式是$S_{扇形}=__________ = __________. $
答案:
(1)半径 弧
(2)$\frac{n\pi r^{2}}{360}$ $\frac{1}{2}lr$
(1)半径 弧
(2)$\frac{n\pi r^{2}}{360}$ $\frac{1}{2}lr$
例2 (1)在圆心角为120°的扇形AOB中,半径OA = 6cm,则扇形AOB的面积是( )
A. 6πcm² B. 8πcm² C. 12πcm² D. 24πcm²
A. 6πcm² B. 8πcm² C. 12πcm² D. 24πcm²
答案:
(1)C
(1)C
(2)已知扇形的半径为6cm,面积为10πcm²,求该扇形的弧长.
答案:
(2)$\frac{10\pi}{3}$ cm
(2)$\frac{10\pi}{3}$ cm
运用扇形面积公式求弓形的面积
(1)如图27−3−2①,水平放置的圆柱形排水管道的截面半径是0.6m,其中水面最高为0.3m,求截面上有水部分的面积(精确到0.01m²);
(2)如图27−3−2②,水平放置的圆柱形排水管道的截面半径是0.6m,其中水面最高为0.9m,求截面上有水部分的面积(精确到0.01m²).

(1)如图27−3−2①,水平放置的圆柱形排水管道的截面半径是0.6m,其中水面最高为0.3m,求截面上有水部分的面积(精确到0.01m²);
(2)如图27−3−2②,水平放置的圆柱形排水管道的截面半径是0.6m,其中水面最高为0.9m,求截面上有水部分的面积(精确到0.01m²).

答案:
解:
(1)连结OA,OB,过点O作弦AB的垂线,垂足为D,交$\overset{\frown}{AB}$于点C,连结AC.
$\because OC = 0.6$ m,$DC = 0.3$ m,
$\therefore OD = OC - DC = 0.3$ m,即$OD = DC$.
又$AD\perp OC$,$\therefore AD$是线段OC的垂直平分线.
$\therefore AC = AO = OC$.$\therefore\triangle AOC$是等边三角形.
$\therefore\angle AOD = 60^{\circ}$,$\angle AOB = 120^{\circ}$.
故截面上有水部分的面积$= S_{扇形AOB}-S_{\triangle AOB}=\frac{120\pi}{360}\times0.6^{2}-\frac{1}{2}AB\cdot OD = 0.12\pi-\frac{1}{2}\times0.6\times\sqrt{3}\times0.3\approx0.22(m^{2})$.
(2)连结OA,OB,过点O作弦AB的垂线,垂足为E,交$\odot O$于D,C两点,如图.
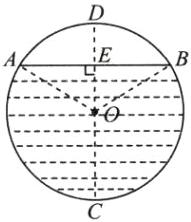
由题意可知,$OE = CE - OC = 0.9 - 0.6 = 0.3$ (m),易得$\angle BOE = 60^{\circ}$,$\angle AOB = 120^{\circ}$,$\overset{\frown}{ACB}$所对的圆心角为$240^{\circ}$.
故截面上有水部分的面积为$\frac{240\pi}{360}\times0.6^{2}+\frac{1}{2}\times0.6\times\sqrt{3}\times0.3 = 0.24\pi + 0.09\times\sqrt{3}\approx0.91(m^{2})$.
解:
(1)连结OA,OB,过点O作弦AB的垂线,垂足为D,交$\overset{\frown}{AB}$于点C,连结AC.
$\because OC = 0.6$ m,$DC = 0.3$ m,
$\therefore OD = OC - DC = 0.3$ m,即$OD = DC$.
又$AD\perp OC$,$\therefore AD$是线段OC的垂直平分线.
$\therefore AC = AO = OC$.$\therefore\triangle AOC$是等边三角形.
$\therefore\angle AOD = 60^{\circ}$,$\angle AOB = 120^{\circ}$.
故截面上有水部分的面积$= S_{扇形AOB}-S_{\triangle AOB}=\frac{120\pi}{360}\times0.6^{2}-\frac{1}{2}AB\cdot OD = 0.12\pi-\frac{1}{2}\times0.6\times\sqrt{3}\times0.3\approx0.22(m^{2})$.
(2)连结OA,OB,过点O作弦AB的垂线,垂足为E,交$\odot O$于D,C两点,如图.

由题意可知,$OE = CE - OC = 0.9 - 0.6 = 0.3$ (m),易得$\angle BOE = 60^{\circ}$,$\angle AOB = 120^{\circ}$,$\overset{\frown}{ACB}$所对的圆心角为$240^{\circ}$.
故截面上有水部分的面积为$\frac{240\pi}{360}\times0.6^{2}+\frac{1}{2}\times0.6\times\sqrt{3}\times0.3 = 0.24\pi + 0.09\times\sqrt{3}\approx0.91(m^{2})$.
1. 已知扇形的圆心角为120°,半径为3 cm,则弧长为( )
A. $\frac{2\pi}{3}$ cm
B. 2π cm
C. 4π cm
D. $\frac{\pi}{3}$ cm
A. $\frac{2\pi}{3}$ cm
B. 2π cm
C. 4π cm
D. $\frac{\pi}{3}$ cm
答案:
B
2. 一个扇形的弧长为3π cm,半径为4 cm,则该扇形的面积为________cm².
答案:
$6\pi$
3. 如图27 - 3 - 4,已知扇形AOB的半径为2,圆心角为90°,连结AB,则图中阴影部分的面积是________.


答案:
$\pi - 2$
查看更多完整答案,请扫码查看


