《2025年全品学练考九年级数学下册华师大版》

模块1 与圆有关的概念
连结圆上任意两点的______叫做弦，经过圆心的弦叫做______，顶点在圆心的角叫做______，圆上任意两点间的部分叫做圆弧，简称______，圆的任意一条直径的两个端点把圆分成两个______，大于半圆的弧叫做______，小于半圆的弧叫做______，在同圆或等圆中，能够互相重合的弧叫做______．

答案： 线段　直径　圆心角　弧　半圆　优弧　劣弧　等弧

例1 有下列说法：①圆中最长的弦不一定是直径；②同一个圆中，优弧大于半圆周，劣弧小于半圆周；③等弧的长度一定相等；④经过圆内一个定点可以作无数条弦；⑤经过圆内一个定点可以作无数条直径．其中正确的有（ ）
A. 1个
B. 2个
C. 3个
D. 4个

答案： C

模块2 圆心角、弧、弦之间的关系
在同一个圆中，如果圆心角相等，那么它们所对的弧______，所对的弦______．
在同一个圆中，如果弧相等，那么它们所对的圆心角______，所对的弦______．
在同一个圆中，如果弦相等，那么它们所对的圆心角______，所对的弧______．

答案： 相等　相等　相等　相等　相等　相等

例2 如图27 - T - 1，在⊙O中，AB，CD是两条弦，OM⊥CD，ON⊥AB，垂足分别为M，N．若AB = CD，则下列结论不正确的是（ ）

A. ∠AON = ∠DOM
B. AN = DM
C. OM = DM
D. OM = ON

答案： C

模块3 垂径定理及其推论
垂径定理：垂直于弦的直径______这条弦，并且______这条弦所对的两条弧．
推论：平分弦（不是直径）的直径______这条弦，并且______这条弦所对的两条弧；平分弧的直径______这条弧所对的弦．

答案： 平分　平分　垂直于　平分　垂直平分

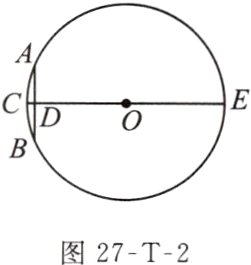
例3 《九章算术》是我国古代著名数学专著，其中有这样一个问题：“今有圆材，埋在壁中，不知大小．以锯锯之，深一寸，锯道长一尺．问径几何．”其意为：今有一圆柱形木材，埋在墙壁中，不知其大小，用锯去锯该木材，锯口深1寸，锯道长1尺．如图27 - T - 2，CE是⊙O的直径，弦AB = 1尺，弓形高CD = 1寸（注：1尺 = 10寸），则这块圆柱形木材的直径是多少寸？

答案： 26寸