例6 如图27 - 1 - 37,点A,B,C,D都在⊙O上,∠ABC = 90°,AD = 12,CD = 5,则⊙O的直径是________.


答案:
13
分类讨论求弦所对的圆周角的度数
已知⊙O的弦AB的长等于⊙O的半径,求此弦AB所对的圆周角的度数.
已知⊙O的弦AB的长等于⊙O的半径,求此弦AB所对的圆周角的度数.
答案:
解:分下面两种情况:如图①,
连结OA,OB,在弦AB所对的优弧上任取一点C,连结CA,CB.
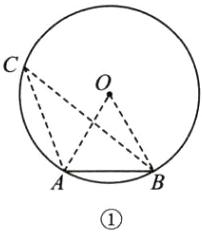
∵AB=OA=OB,
∴△AOB为等边三角形,
∴∠AOB=60°,
∴∠ACB=$\frac{1}{2}$∠AOB=30°,
即弦AB所对的圆周角的度数为30°.
如图②,连结OA,OB,在弦AB所对的劣弧上任取一点D,连结AD,OD,BD,则∠BAD=$\frac{1}{2}$∠BOD,∠ABD=$\frac{1}{2}$∠AOD.
∴∠BAD+∠ABD=$\frac{1}{2}$(∠BOD + ∠AOD)=$\frac{1}{2}$∠AOB.
∵AB=OA=OB,
∴△AOB为等边三角形,
∴∠AOB=60°,
∴∠BAD+∠ABD=30°,
∴∠ADB=180°-(∠BAD+∠ABD)=150°,
即弦AB所对的圆周角的度数为150°.
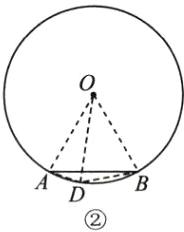
综上所述,弦AB所对的圆周角的度数是30°或150°.
解:分下面两种情况:如图①,
连结OA,OB,在弦AB所对的优弧上任取一点C,连结CA,CB.

∵AB=OA=OB,
∴△AOB为等边三角形,
∴∠AOB=60°,
∴∠ACB=$\frac{1}{2}$∠AOB=30°,
即弦AB所对的圆周角的度数为30°.
如图②,连结OA,OB,在弦AB所对的劣弧上任取一点D,连结AD,OD,BD,则∠BAD=$\frac{1}{2}$∠BOD,∠ABD=$\frac{1}{2}$∠AOD.
∴∠BAD+∠ABD=$\frac{1}{2}$(∠BOD + ∠AOD)=$\frac{1}{2}$∠AOB.
∵AB=OA=OB,
∴△AOB为等边三角形,
∴∠AOB=60°,
∴∠BAD+∠ABD=30°,
∴∠ADB=180°-(∠BAD+∠ABD)=150°,
即弦AB所对的圆周角的度数为150°.

综上所述,弦AB所对的圆周角的度数是30°或150°.
1. 用直角尺检查某圆弧形工件,根据下列检查的结果,能判断该工件一定是半圆的是 ( )


答案:
B
2. 如图27−1−39,在⊙O中,∠BOC = 54°,则∠BAC的度数为( )
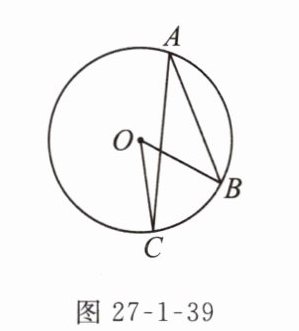
A. 27°
B. 28°
C. 36°
D. 54°

A. 27°
B. 28°
C. 36°
D. 54°
答案:
A
3. 如图27−1−40,△ABC分别交⊙O于点A,B,D,E,且CA = CB,求证:AD = BE.


答案:
证明:
∵CA = CB,
∴∠A = ∠B,
∵$\overset{\frown}{BD}=\overset{\frown}{AE}$,
∴$\overset{\frown}{AE}-\overset{\frown}{DE}=\overset{\frown}{BD}-\overset{\frown}{DE}$,
即$\overset{\frown}{AD}=\overset{\frown}{BE}$,
∴AD = BE.
∵CA = CB,
∴∠A = ∠B,
∵$\overset{\frown}{BD}=\overset{\frown}{AE}$,
∴$\overset{\frown}{AE}-\overset{\frown}{DE}=\overset{\frown}{BD}-\overset{\frown}{DE}$,
即$\overset{\frown}{AD}=\overset{\frown}{BE}$,
∴AD = BE.
4. 如图27−1−41,AB为⊙O的直径,点C,D在⊙O上. 若∠AOD = 30°,求∠BCD的度数.


答案:
$105^{\circ}$
查看更多完整答案,请扫码查看


