[操作发现]
画出函数$y = x^{2}-x-\frac{3}{4}$的图象,根据图象回答下列问题:
(1)图象与x轴交点的坐标是什么?
(2)当x取何值时,y = 0?这里x的取值与方程$x^{2}-x-\frac{3}{4}=0$有什么关系?
(3)你能从中得到什么启发?
画出函数$y = x^{2}-x-\frac{3}{4}$的图象,根据图象回答下列问题:
(1)图象与x轴交点的坐标是什么?
(2)当x取何值时,y = 0?这里x的取值与方程$x^{2}-x-\frac{3}{4}=0$有什么关系?
(3)你能从中得到什么启发?
答案:
解:二次函数$y=x^{2}-x-\frac{3}{4}$的图象如图.
(1)图象与$x$轴的交点坐标是$(\frac{3}{2},0),(-\frac{1}{2},0)$.
(2)当$x = \frac{3}{2}$或$x = -\frac{1}{2}$时,$y = 0$,这里$x$的取值是方程$x^{2}-x-\frac{3}{4}=0$的两个根.
(3)二次函数$y = x^{2}-x-\frac{3}{4}$的图象与$x$轴的交点的横坐标是一元二次方程$x^{2}-x-\frac{3}{4}=0$的两个根,一元二次方程$x^{2}-x-\frac{3}{4}=0$的两个根就是二次函数$y = x^{2}-x-\frac{3}{4}$的图象与$x$轴的交点的横坐标.
解:二次函数$y=x^{2}-x-\frac{3}{4}$的图象如图.
(1)图象与$x$轴的交点坐标是$(\frac{3}{2},0),(-\frac{1}{2},0)$.

(2)当$x = \frac{3}{2}$或$x = -\frac{1}{2}$时,$y = 0$,这里$x$的取值是方程$x^{2}-x-\frac{3}{4}=0$的两个根.
(3)二次函数$y = x^{2}-x-\frac{3}{4}$的图象与$x$轴的交点的横坐标是一元二次方程$x^{2}-x-\frac{3}{4}=0$的两个根,一元二次方程$x^{2}-x-\frac{3}{4}=0$的两个根就是二次函数$y = x^{2}-x-\frac{3}{4}$的图象与$x$轴的交点的横坐标.
二次函数与对应的一元二次方程的联系:二次函数$y = ax^{2}+bx + c$的图象与x轴的交点有三种情况:有两个交点、有一个交点、没有交点.
与此相对应,一元二次方程$ax^{2}+bx + c = 0$的根也有三种情况:有__________实数根、有__________实数根、________实数根.
二次函数$y = ax^{2}+bx + c$的图象与x轴交点的________就是一元二次方程$ax^{2}+bx + c = 0$的根.
与此相对应,一元二次方程$ax^{2}+bx + c = 0$的根也有三种情况:有__________实数根、有__________实数根、________实数根.
二次函数$y = ax^{2}+bx + c$的图象与x轴交点的________就是一元二次方程$ax^{2}+bx + c = 0$的根.
答案:
两个不相等的 两个相等的 没有 横坐标
例1 在平面直角坐标系中,二次函数$y = x^{2}+bx + c$的部分图象如图26 - 3 - 4所示,则关于x的方程$x^{2}+bx + c = 0$的解是________.
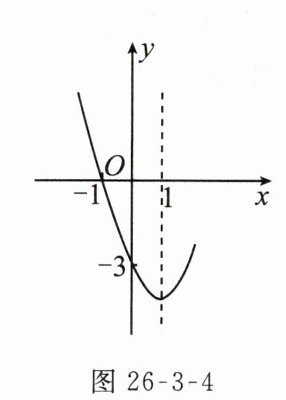

答案:
$x_{1}=-1,x_{2}=3$
变式 如图26 - 3 - 5,在平面直角坐标系中,抛物线$y = 2x^{2}$与直线$y = 3x + 2$相交于点$A(-\frac{1}{2},\frac{1}{2}),B(2,8)$,则方程$2x^{2}-3x - 2 = 0$的解为________.
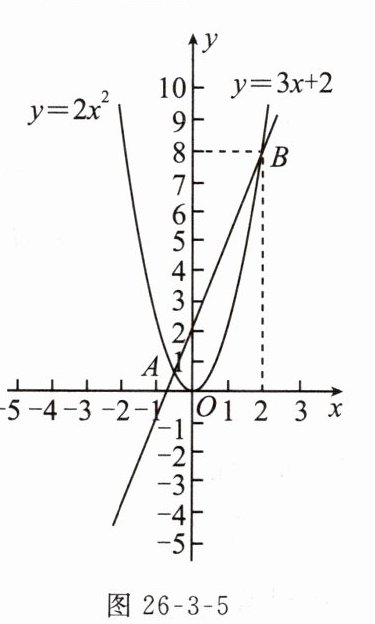

答案:
$x_{1}=-\frac{1}{2},x_{2}=2$
例2 若抛物线$y = x^{2}-2x - m$与x轴有两个交点,则m的取值范围是________.
答案:
$m > -1$
查看更多完整答案,请扫码查看


