《2025年全品学练考九年级数学下册华师大版》

[操作发现]
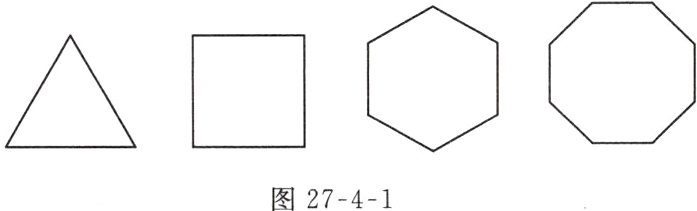
分别画出图27 - 4 - 1中各正多边形的对称轴，看看能发现什么结果？

答案： [操作发现]
解:图略，一个正n边形共有n条对称轴.

[归纳推理]
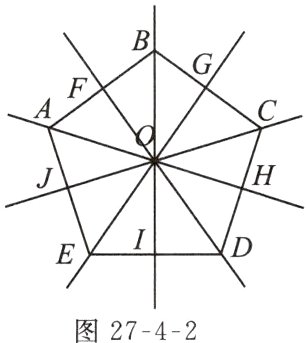
1. 观察如图27 - 4 - 2所示的正五边形的各条对称轴.
(1)是否存在一个圆经过正五边形的各顶点？如果存在，请说明理由；
(2)是否存在一个圆与正五边形各边相切？如果存在，请说明理由.

2. 其他的正多边形，是否也能得出同样的第1题中(1)(2)中的结论？

答案： [归纳推理]
1.解:
(1)存在.理由:易知点O是正五边形各边的垂直平分线的交点，则点O到正五边形各个顶点的距离相等，记作R.那么以点O为圆心，R为半径的圆就过正五边形的各个顶点.
(2)存在.理由:这些对称轴是正五边形各内角的平分线，则点O到正五边形各边的距离相等，记作r，那么以点O为圆心，r为半径的圆与正五边形的各边都相切.
2.解:也能得到同样的第1题中
(1)
(2)中的结论.

[概括新知]
(1)正多边形与圆的关系：任何正多边形都有一个________和一个________.
(2)正多边形的有关概念：
正多边形的中心：正多边形的__________(或内切圆)的圆心叫做正多边形的中心.
正多边形的半径：外接圆的________叫做正多边形的半径.
正多边形的边心距：________的半径叫做正多边形的边心距.
正多边形的中心角：正多边形每一条边所对的外接圆的圆心角都相等，叫做正多边形的中心角. 正n(n≥3，且n为整数)边形的每个中心角都等于________.

答案： [概括新知]
(1)外接圆　内切圆
(2)外接圆　半径　内切圆　$\frac{360^{\circ}}{n}$