1. 已知函数$y = -2(x + 1)^2 - 1$,其图象大致是( }


答案:
C
2. 在平面直角坐标系中,将抛物线$y = (x + 1)^2$向右平移2个单位,再向下平移4个单位,得到的抛物线的函数表达式是( )
A. $y = (x - 2)^2 - 4$
B. $y = (x - 1)^2 - 4$
C. $y = (x - 2)^2 - 3$
D. $y = (x - 1)^2 - 3$
A. $y = (x - 2)^2 - 4$
B. $y = (x - 1)^2 - 4$
C. $y = (x - 2)^2 - 3$
D. $y = (x - 1)^2 - 3$
答案:
B
3. 已知二次函数$y = (x - 2)^2 + 2$,若点$(3,y_1)$,$(2.5,y_2)$,$(4,y_3)$在函数图象上,则$y_1$,$y_2$,$y_3$的大小关系正确的是( )
A. $y_3 < y_1 < y_2$
B. $y_2 < y_1 < y_3$
C. $y_3 < y_2 < y_1$
D. $y_1 < y_2 < y_3$
A. $y_3 < y_1 < y_2$
B. $y_2 < y_1 < y_3$
C. $y_3 < y_2 < y_1$
D. $y_1 < y_2 < y_3$
答案:
B
4. 已知抛物线$y = -\frac{1}{4}(x - 2)^2 + 3$.
(1)写出该抛物线的开口方向、对称轴和顶点坐标;
(2)当$y$随$x$的增大而增大时,求$x$的取值范围;
(3)当$1 < x < 4$时,求$y$的取值范围.
(1)写出该抛物线的开口方向、对称轴和顶点坐标;
(2)当$y$随$x$的增大而增大时,求$x$的取值范围;
(3)当$1 < x < 4$时,求$y$的取值范围.
答案:
(1)该抛物线的开口向下,对称轴为直线$x = 2$,顶点坐标为$(2,3)$。
(2)当$x
(1)该抛物线的开口向下,对称轴为直线$x = 2$,顶点坐标为$(2,3)$。
(2)当$x
探究 二次函数$y=ax^{2}+bx+c$的图象与性质
[操作发现]
已知二次函数$y=-\frac{1}{2}x^{2}+x-\frac{5}{2}$.
(1)请将该函数化成$y=a(x - h)^{2} + k$的形式,说出这个函数图象的开口方向、对称轴和顶点坐标;
(2)在平面直角坐标系中画出该二次函数的图象;
(3)由图象你能发现这个函数具有哪些性质?
[操作发现]
已知二次函数$y=-\frac{1}{2}x^{2}+x-\frac{5}{2}$.
(1)请将该函数化成$y=a(x - h)^{2} + k$的形式,说出这个函数图象的开口方向、对称轴和顶点坐标;
(2)在平面直角坐标系中画出该二次函数的图象;
(3)由图象你能发现这个函数具有哪些性质?
答案:
[操作发现]
解:
(1)因为y = -$\frac{1}{2}$x² + x - $\frac{5}{2}$ = -$\frac{1}{2}$(x - 1)² - 2,所以这个函数图象的开口向下,对称轴为直线x = 1,顶点坐标为(1, -2)。
(2)略。
(3)当x < 1时,函数值y随x的增大而增大;当x > 1时,函数值y随x的增大而减小;当x = 1时,函数取得最大值,最大值为 -2。
解:
(1)因为y = -$\frac{1}{2}$x² + x - $\frac{5}{2}$ = -$\frac{1}{2}$(x - 1)² - 2,所以这个函数图象的开口向下,对称轴为直线x = 1,顶点坐标为(1, -2)。
(2)略。
(3)当x < 1时,函数值y随x的增大而增大;当x > 1时,函数值y随x的增大而减小;当x = 1时,函数取得最大值,最大值为 -2。
[转化归纳]
对于任意一个二次函数$y=ax^{2}+bx+c(a≠0)$.
(1)请你利用配方法将其化成$y=a(x - h)^{2} + k$的形式;
(2)说一说如何确定二次函数图象的开口方向、对称轴和顶点坐标?
对于任意一个二次函数$y=ax^{2}+bx+c(a≠0)$.
(1)请你利用配方法将其化成$y=a(x - h)^{2} + k$的形式;
(2)说一说如何确定二次函数图象的开口方向、对称轴和顶点坐标?
答案:
[转化归纳]
解:
(1)y = ax² + bx + c = a(x² + $\frac{b}{a}$x + $\frac{c}{a}$) = a[x² + 2·$\frac{b}{2a}$x + ($\frac{b}{2a}$)² - ($\frac{b}{2a}$)² + $\frac{c}{a}$] = a(x + $\frac{b}{2a}$)² + $\frac{4ac - b²}{4a}$。
(2)二次函数图象的开口方向由a的正负决定,当a > 0时,抛物线开口向上;当a < 0时,抛物线开口向下。二次函数图象的对称轴和顶点坐标的确定有两种方法:方法一:配方法,将二次函数配方成顶点式y = a(x - h)² + k,从而确定抛物线的对称轴和顶点坐标;方法二:公式法,二次函数图象的对称轴为直线x = -$\frac{b}{2a}$,顶点坐标为(-$\frac{b}{2a}$,$\frac{4ac - b²}{4a}$)。
解:
(1)y = ax² + bx + c = a(x² + $\frac{b}{a}$x + $\frac{c}{a}$) = a[x² + 2·$\frac{b}{2a}$x + ($\frac{b}{2a}$)² - ($\frac{b}{2a}$)² + $\frac{c}{a}$] = a(x + $\frac{b}{2a}$)² + $\frac{4ac - b²}{4a}$。
(2)二次函数图象的开口方向由a的正负决定,当a > 0时,抛物线开口向上;当a < 0时,抛物线开口向下。二次函数图象的对称轴和顶点坐标的确定有两种方法:方法一:配方法,将二次函数配方成顶点式y = a(x - h)² + k,从而确定抛物线的对称轴和顶点坐标;方法二:公式法,二次函数图象的对称轴为直线x = -$\frac{b}{2a}$,顶点坐标为(-$\frac{b}{2a}$,$\frac{4ac - b²}{4a}$)。
[概括新知]
二次函数$y=ax^{2}+bx+c$的图像与性质
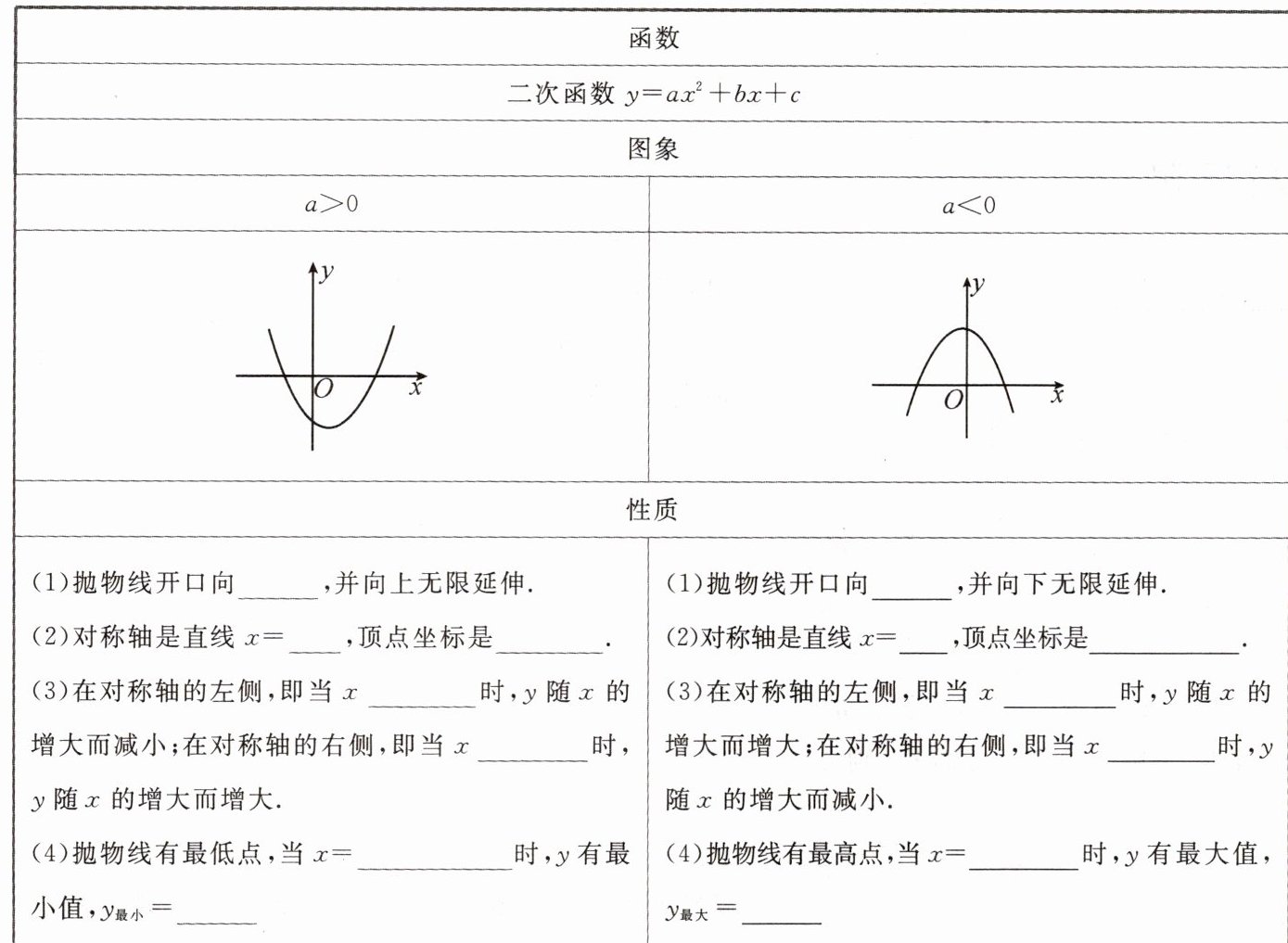
二次函数$y=ax^{2}+bx+c$的图像与性质

答案:
[概括新知] 上 $-\frac{b}{2a}$ $(-\frac{b}{2a},\frac{4ac - b^{2}}{4a})$ $<-\frac{b}{2a}$ $>-\frac{b}{2a}$ $-\frac{b}{2a}$ $\frac{4ac - b^{2}}{4a}$ 下 $-\frac{b}{2a}$ $(-\frac{b}{2a},\frac{4ac - b^{2}}{4a})$ $<-\frac{b}{2a}$ $>-\frac{b}{2a}$ $-\frac{b}{2a}$ $\frac{4ac - b^{2}}{4a}$
查看更多完整答案,请扫码查看


