2025年金考卷中考45套汇编数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年金考卷中考45套汇编数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第98页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
8. 在平面直角坐标系$xOy$中,点$A$的坐标为$(3,0)$,点$B$的坐标为$(2,-2)$,将线段$AB$平移得到线段$CD$,点$A$的对应点$C$的坐标为$(3,5)$,则点$B$的对应点$D$的坐标为(
A.$(7,-2)$
B.$(2,3)$
C.$(2,-7)$
D.$(-3,-2)$
B
)A.$(7,-2)$
B.$(2,3)$
C.$(2,-7)$
D.$(-3,-2)$
答案:
8 B $\because$点$A(3,0)$平移后得到点$C(3,5)$,$\therefore$线段AB向上平移5个单位长度得到线段CD,$\therefore$点$B(2,-2)$的对应点D的坐标为$(2,3)$.
9. 中国古代数学家杨辉的《田亩比类乘除捷法》中记载:“直田积八百六十四步,只云长阔共六十步,问长多阔几何.”其大意是:一块矩形田地的面积为864平方步,只知道它的长与宽共60步,问它的长比宽多多少步?设这个矩形的宽为$x$步,根据题意可列方程为(
A.$x(60 - x) = 864$
B.$x(x - 60) = 864$
C.$x(60 + x) = 864$
D.$2[x + (x + 60)] = 864$
A
)A.$x(60 - x) = 864$
B.$x(x - 60) = 864$
C.$x(60 + x) = 864$
D.$2[x + (x + 60)] = 864$
答案:
9 A
10. 如图,在$\triangle ABC$中,$AB = 16$,$BC = 12$,$CA = 10$,$\angle ABC$的平分线$BP$与$AC$相交于点$D$.在线段$AD$上取一点$K$,以点$C$为圆心,$CK$长为半径作弧,与射线$BP$相交于点$M$和点$N$,再分别以点$M$和点$N$为圆心,大于$\frac{1}{2}MN$的长为半径作弧,两弧相交于点$Q$,作射线$CQ$,与$AB$相交于点$E$,连接$DE$,则$\triangle DAE$的周长为(
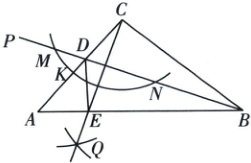
A.$12$
B.$14$
C.$16$
D.$18$
B
)
A.$12$
B.$14$
C.$16$
D.$18$
答案:
10 B 如图,设CE,BD交于点O. $\because BP$平分$\angle ABC$,$\therefore \angle 1 = \angle 2$.由作图可知,$CE \perp BD$,$\therefore \angle BOC = \angle BOE = 90^{\circ}$.
又$\because BO = BO$,$\therefore \triangle BOC \cong \triangle BOE(ASA)$,$\therefore BE = BC = 12$,
$OC = OE$,$\therefore AE = 16 - 12 = 4$,BD是CE的垂直平分线,$\therefore DE = DC$,$\therefore \triangle DAE$的周长为$AD + DE + AE = AD + DC + AE = AC + AE = 10 + 4 = 14$.

10 B 如图,设CE,BD交于点O. $\because BP$平分$\angle ABC$,$\therefore \angle 1 = \angle 2$.由作图可知,$CE \perp BD$,$\therefore \angle BOC = \angle BOE = 90^{\circ}$.
又$\because BO = BO$,$\therefore \triangle BOC \cong \triangle BOE(ASA)$,$\therefore BE = BC = 12$,
$OC = OE$,$\therefore AE = 16 - 12 = 4$,BD是CE的垂直平分线,$\therefore DE = DC$,$\therefore \triangle DAE$的周长为$AD + DE + AE = AD + DC + AE = AC + AE = 10 + 4 = 14$.

11. 在乒乓球质量检测中,如果一只乒乓球的质量超出标准质量$0.02g$记作$+0.02g$,那么低于标准质量$0.01g$记作
-0.01
g.
答案:
$-0.01$
12. 在电压不变的情况下,电流$I$(单位:$A$)与电阻$R$(单位:$\Omega$)是反比例函数关系.当$R = 4$时,$I = 5$,则电流$I$与电阻$R$之间的函数表达式为$I =$
$\frac{20}{R}$
.
答案:
$\frac{20}{R}$
13. 甲、乙两名运动员进行跳远测试,每人测试10次,他们各自测试成绩(单位:$cm$)的平均数和方差如下表:
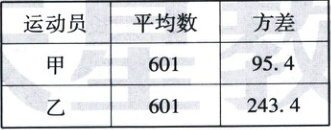
则这两名运动员测试成绩更稳定的是

则这两名运动员测试成绩更稳定的是
甲
(填“甲”或“乙”).
答案:
甲
14. 如图,为了测量树$AB$的高度,在水平地面上取一点$C$,在$C$处测得$\angle ACB = 51^{\circ}$,$BC = 6m$,则树$AB$的高约为
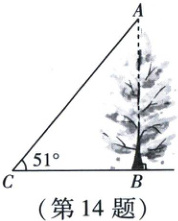
7.4
m(结果精确到$0.1m$.参考数据:$\sin51^{\circ}\approx0.78$,$\cos51^{\circ}\approx0.63$,$\tan51^{\circ}\approx1.23$).
答案:
14 7.4
【解析】在$Rt \triangle ABC$中,$\because \tan \angle ACB = \frac{AB}{BC}$,$\therefore AB = BC · \tan \angle ACB \approx 6 × 1.23 \approx 7.4( m)$.
【解析】在$Rt \triangle ABC$中,$\because \tan \angle ACB = \frac{AB}{BC}$,$\therefore AB = BC · \tan \angle ACB \approx 6 × 1.23 \approx 7.4( m)$.
15. 如图,在菱形$ABCD$中,对角线$AC$与$BD$相交于点$O$,$AC = 8$,$BD = 12$,点$E$在线段$OA$上,$AE = 2$,点$F$在线段$OC$上,$OF = 1$,连接$BE$,点$G$为$BE$的中点,连接$FG$,则$FG$的长为
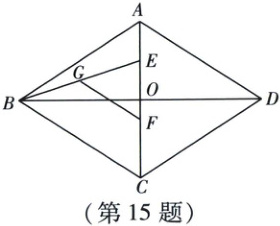
$\sqrt{13}$
.
答案:
15 $\sqrt{13}$
【解析】$\because$四边形ABCD是菱形,$\therefore AC \perp BD$,$OA = OC = \frac{1}{2}AC = 4$,$OB = OD = \frac{1}{2}BD = 6$,$\therefore BC = \sqrt{OB^{2} + OC^{2}} = \sqrt{6^{2} + 4^{2}} = 2\sqrt{13}$.又$\because AE = 2$,$OF = 1$,$\therefore OE = 4 - 2 = 2$,$FC = 4 - 1 = 3$,$\therefore EF = 2 + 1 = 3$,$\therefore EF = FC$.又$\because$点G为BE的中点,$\therefore GF$是$\triangle EBC$的中位线,$\therefore GF = \frac{1}{2}BC = \sqrt{13}$.
一题多解
利用坐标求解.如图,以点O为原点,直线BD为x轴,建立平面直角坐标系,易知$E(0,2)$,$F(0,-1)$,$B(-6,0)$. $\because$点G为BE的中点,$\therefore G(-3,1)$,$\therefore FG = \sqrt{(-3)^{2} + (1 + 1)^{2}} = \sqrt{13}$.

名师敲重点
知识积累
菱形的性质
1. 边:菱形的对边平行,四条边相等.
2. 角:菱形的对角相等.
3. 对角线:菱形的对角线互相垂直平分,并且每一条对角线平分一组对角.
4. 对称性:菱形既是轴对称图形,也是中心对称图形.
15 $\sqrt{13}$
【解析】$\because$四边形ABCD是菱形,$\therefore AC \perp BD$,$OA = OC = \frac{1}{2}AC = 4$,$OB = OD = \frac{1}{2}BD = 6$,$\therefore BC = \sqrt{OB^{2} + OC^{2}} = \sqrt{6^{2} + 4^{2}} = 2\sqrt{13}$.又$\because AE = 2$,$OF = 1$,$\therefore OE = 4 - 2 = 2$,$FC = 4 - 1 = 3$,$\therefore EF = 2 + 1 = 3$,$\therefore EF = FC$.又$\because$点G为BE的中点,$\therefore GF$是$\triangle EBC$的中位线,$\therefore GF = \frac{1}{2}BC = \sqrt{13}$.
一题多解
利用坐标求解.如图,以点O为原点,直线BD为x轴,建立平面直角坐标系,易知$E(0,2)$,$F(0,-1)$,$B(-6,0)$. $\because$点G为BE的中点,$\therefore G(-3,1)$,$\therefore FG = \sqrt{(-3)^{2} + (1 + 1)^{2}} = \sqrt{13}$.

名师敲重点
知识积累
菱形的性质
1. 边:菱形的对边平行,四条边相等.
2. 角:菱形的对角相等.
3. 对角线:菱形的对角线互相垂直平分,并且每一条对角线平分一组对角.
4. 对称性:菱形既是轴对称图形,也是中心对称图形.
16. (10分)
(1)(5分)计算:$3^{2} + (-1)×4 + \sqrt[3]{-27} + |-2|$;
(2)(5分)计算:$\frac{1}{m + 1}÷\frac{m^{3}}{m^{2} + 2m + 1} - \frac{1}{m^{3}}$.
(1)(5分)计算:$3^{2} + (-1)×4 + \sqrt[3]{-27} + |-2|$;
(2)(5分)计算:$\frac{1}{m + 1}÷\frac{m^{3}}{m^{2} + 2m + 1} - \frac{1}{m^{3}}$.
答案:
16
(1)原式$=9 - 4 - 3 + 2$
$=4$. (4分)
(2)原式$=\frac{1}{m + 1} · \frac{(m + 1)^{2}}{m^{3}} - \frac{1}{m^{3}}$ (2分)
$=\frac{m + 1}{m^{3}} - \frac{1}{m^{3}}$ (3分)
$=\frac{m}{m^{3}}$
$=\frac{1}{m^{2}}$. (4分)
(1)原式$=9 - 4 - 3 + 2$
$=4$. (4分)
(2)原式$=\frac{1}{m + 1} · \frac{(m + 1)^{2}}{m^{3}} - \frac{1}{m^{3}}$ (2分)
$=\frac{m + 1}{m^{3}} - \frac{1}{m^{3}}$ (3分)
$=\frac{m}{m^{3}}$
$=\frac{1}{m^{2}}$. (4分)
查看更多完整答案,请扫码查看


