2025年金考卷中考45套汇编数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年金考卷中考45套汇编数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第119页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
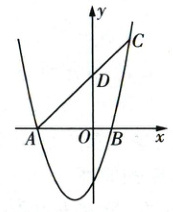
24. (11 分)在平面直角坐标系中,抛物线 $y = ax^{2} + bx - 3(a\neq 0)$ 与 $x$ 轴交于 $A$,$B$ 两点,点 $B$ 的坐标为 $(1,0)$,点 $C(2,5)$ 在抛物线上.
(1) 求抛物线的解析式.
(2) ①求点 $A$ 的坐标;
②当 $y < 0$ 时,根据图象直接写出 $x$ 的取值范围:
(3) 连接 $AC$ 交 $y$ 轴于点 $D$,在 $y$ 轴上是否存在点 $P$,使 $\triangle ACP$ 是以 $AC$ 为直角边的直角三角形,若存在,请直接写出所有符合条件的点 $P$ 坐标,若不存在,请说明理由.
(1) 求抛物线的解析式.
(2) ①求点 $A$ 的坐标;
②当 $y < 0$ 时,根据图象直接写出 $x$ 的取值范围:
-3<x<1
.(3) 连接 $AC$ 交 $y$ 轴于点 $D$,在 $y$ 轴上是否存在点 $P$,使 $\triangle ACP$ 是以 $AC$ 为直角边的直角三角形,若存在,请直接写出所有符合条件的点 $P$ 坐标,若不存在,请说明理由.

答案:
(1)将B(1,0),C(2,5)代入$y=ax^2+bx - 3$
得$\begin{cases}a + b - 3 = 0, \\4a + 2b - 3 = 5,\end{cases}$ (2分)
解得$\begin{cases}a = 1, \\ b = 2,\end{cases}$ (3分)
∴抛物线的解析式为$y=x^2+2x - 3$。 (4分)
(2)①当y=0时,$x^2+2x - 3 = 0$,
得$x_1=-3,x_2=1$,
∴A(-3,0)。 (6分)
②-3<x<1。 (7分)
(3)存在,$P_1(0,7),P_2(0,-3)$。 (11分)
解法提示:
以AC为直角边的直角三角形分点A为直角顶点,点C为直角顶点两种情况,如图。

设P(0,p)。
∵A(-3,0),C(2,5),
∴$AP^2=3^2+p^2=9+p^2$,$CP^2=2^2+(5 - p)^2=29 - 10p+p^2$,
$AC^2=(2 + 3)^2+5^2=50$。
当点A为直角顶点时,则$AC^2+AP^2=CP^2$,
∴$50+9+p^2=29 - 10p+p^2$,解得p=-3。
当点C为直角顶点时,则$AC^2+CP^2=AP^2$,
∴$50+29 - 10p+p^2=9+p^2$,解得p=7。
综上点P的坐标为(0,7)或(0,-3)。
(1)将B(1,0),C(2,5)代入$y=ax^2+bx - 3$
得$\begin{cases}a + b - 3 = 0, \\4a + 2b - 3 = 5,\end{cases}$ (2分)
解得$\begin{cases}a = 1, \\ b = 2,\end{cases}$ (3分)
∴抛物线的解析式为$y=x^2+2x - 3$。 (4分)
(2)①当y=0时,$x^2+2x - 3 = 0$,
得$x_1=-3,x_2=1$,
∴A(-3,0)。 (6分)
②-3<x<1。 (7分)
(3)存在,$P_1(0,7),P_2(0,-3)$。 (11分)
解法提示:
以AC为直角边的直角三角形分点A为直角顶点,点C为直角顶点两种情况,如图。

设P(0,p)。
∵A(-3,0),C(2,5),
∴$AP^2=3^2+p^2=9+p^2$,$CP^2=2^2+(5 - p)^2=29 - 10p+p^2$,
$AC^2=(2 + 3)^2+5^2=50$。
当点A为直角顶点时,则$AC^2+AP^2=CP^2$,
∴$50+9+p^2=29 - 10p+p^2$,解得p=-3。
当点C为直角顶点时,则$AC^2+CP^2=AP^2$,
∴$50+29 - 10p+p^2=9+p^2$,解得p=7。
综上点P的坐标为(0,7)或(0,-3)。
25. (11 分)新课标 项目式学习 活动与探究
解码蜜蜂的“家”——为什么蜂房是正六边形的?
蜜蜂的“集体宿舍”是由多个正六边形密铺在一起的,这些密铺的正六边形使得蜂房之间没有空隙,一点儿也不浪费空间. 这是数学中的密铺(或镶嵌)问题. 平面图形的密铺(或镶嵌)是指用形状、大小完全相同的一种或多种平面图形进行拼接,使彼此之间不留空隙、不重叠地铺成一片.
探究一:若只用一种正多边形,哪些正多边形可以密铺?


(1) 请补全上述表格①
探究二:在能密铺的正多边形中,哪种形状最省材料?
数学视角:蜜蜂的身体可近似看成圆柱,若圆柱底面半径为 1,当蜂房恰好容纳一只蜜蜂即正多边形的内切圆半径均为 1 时,比较正三角形,正方形和正六边形周长的大小.
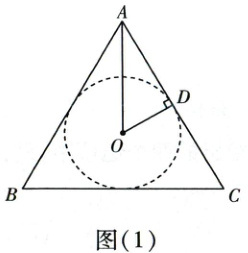
观察图(1),发现 $\odot O$ 是正三角形 $ABC$ 的内切圆,与 $AC$ 切于点 $D$,$OD\perp AD$,$∠OAD = 30^{\circ}$,$OD = 1$,在 $Rt\triangle ADO$ 中,$AD = \sqrt{3}$,则 $\triangle ABC$ 的周长为 $6\sqrt{3}$.
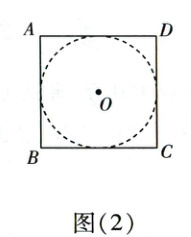
(2) 如图(2),正方形 $ABCD$ 的周长为
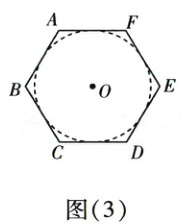
(3) 如图(3),求出正六边形的周长(写出求解过程).
探究三:在能密铺的正多边形中,哪种形状可以使蜜蜂的活动空间最大?
数学视角:假设蜜蜂建造蜂房的材料总量即周长一定,比较正三角形、正方形和正六边形面积的大小.
(4) 若正多边形的周长都为 12,则正三角形的面积为
【得出结论】
综上所述:在相同条件下,正六边形结构最省材料,能使蜜蜂的活动空间最大,是建造蜂房的最优方案.
解码蜜蜂的“家”——为什么蜂房是正六边形的?

蜜蜂的“集体宿舍”是由多个正六边形密铺在一起的,这些密铺的正六边形使得蜂房之间没有空隙,一点儿也不浪费空间. 这是数学中的密铺(或镶嵌)问题. 平面图形的密铺(或镶嵌)是指用形状、大小完全相同的一种或多种平面图形进行拼接,使彼此之间不留空隙、不重叠地铺成一片.
探究一:若只用一种正多边形,哪些正多边形可以密铺?


(1) 请补全上述表格①
90°
;②$360°÷90°=4$
;③$360°÷135°=\frac{8}{3}$
;④不能
.探究二:在能密铺的正多边形中,哪种形状最省材料?
数学视角:蜜蜂的身体可近似看成圆柱,若圆柱底面半径为 1,当蜂房恰好容纳一只蜜蜂即正多边形的内切圆半径均为 1 时,比较正三角形,正方形和正六边形周长的大小.



观察图(1),发现 $\odot O$ 是正三角形 $ABC$ 的内切圆,与 $AC$ 切于点 $D$,$OD\perp AD$,$∠OAD = 30^{\circ}$,$OD = 1$,在 $Rt\triangle ADO$ 中,$AD = \sqrt{3}$,则 $\triangle ABC$ 的周长为 $6\sqrt{3}$.
(2) 如图(2),正方形 $ABCD$ 的周长为
8
;(3) 如图(3),求出正六边形的周长(写出求解过程).
探究三:在能密铺的正多边形中,哪种形状可以使蜜蜂的活动空间最大?
数学视角:假设蜜蜂建造蜂房的材料总量即周长一定,比较正三角形、正方形和正六边形面积的大小.
(4) 若正多边形的周长都为 12,则正三角形的面积为
$4\sqrt{3}$
;正方形的面积为9
;正六边形的面积为$6\sqrt{3}$
.【得出结论】
综上所述:在相同条件下,正六边形结构最省材料,能使蜜蜂的活动空间最大,是建造蜂房的最优方案.


答案:
(1)①90° ②$360°÷90°=4$ ③$360°÷135°=\frac{8}{3}$ ④不能 (4分)
(2)8 (5分)
(3)如图,正六边形的内切圆⊙O与CD切于点M,连接OM,OD,

∴OM⊥CD且OM=1,∠ODM=$\frac{1}{2}$∠CDE=60°。
在Rt△MOD中,∠OMD=90°,∠ODM=60°,
$\tan60°=\frac{OM}{MD}=\frac{1}{MD}=\sqrt{3}$,
∴$MD=\frac{\sqrt{3}}{3}$,
∴$CD=2MD=\frac{2\sqrt{3}}{3}$,
∴$C_{正六边形ABCDEF}=6×\frac{2\sqrt{3}}{3}=4\sqrt{3}$。 (8分)
(4)$4\sqrt{3}$ $9$ $6\sqrt{3}$ (11分)
解法提示:正三角形的周长为12,得其边长为4,则其面积为$\frac{\sqrt{3}}{4}×4^2=4\sqrt{3}$。
正方形的周长为12,得其边长为3,则其面积为9。
正六边形的周长为12,得其边长为2,
则易知其面积为$6×\frac{\sqrt{3}}{4}×2^2=6\sqrt{3}$。
(1)①90° ②$360°÷90°=4$ ③$360°÷135°=\frac{8}{3}$ ④不能 (4分)
(2)8 (5分)
(3)如图,正六边形的内切圆⊙O与CD切于点M,连接OM,OD,

∴OM⊥CD且OM=1,∠ODM=$\frac{1}{2}$∠CDE=60°。
在Rt△MOD中,∠OMD=90°,∠ODM=60°,
$\tan60°=\frac{OM}{MD}=\frac{1}{MD}=\sqrt{3}$,
∴$MD=\frac{\sqrt{3}}{3}$,
∴$CD=2MD=\frac{2\sqrt{3}}{3}$,
∴$C_{正六边形ABCDEF}=6×\frac{2\sqrt{3}}{3}=4\sqrt{3}$。 (8分)
(4)$4\sqrt{3}$ $9$ $6\sqrt{3}$ (11分)
解法提示:正三角形的周长为12,得其边长为4,则其面积为$\frac{\sqrt{3}}{4}×4^2=4\sqrt{3}$。
正方形的周长为12,得其边长为3,则其面积为9。
正六边形的周长为12,得其边长为2,
则易知其面积为$6×\frac{\sqrt{3}}{4}×2^2=6\sqrt{3}$。
查看更多完整答案,请扫码查看


