《2025年金考卷中考45套汇编数学》

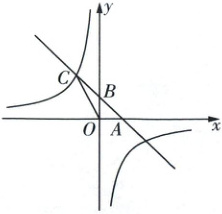
19. （7 分）如图，直线 $y = -x + b$ 与 $x$ 轴交于点 $A(1,0)$，与 $y$ 轴交于点 $B$，与反比例函数 $y = \frac{m}{x}$（$m$ 为常数，$m\neq 0$）的图象在第二象限交于点 $C(-1,a)$.
(1) 求反比例函数的解析式；
(2) 求 $\triangle BOC$ 的面积.

答案：

(1)把点A(1,0)代入$y=-x + b$，得$0=-1 + b$，$b = 1$。(1分)
∴一次函数解析式为$y=-x + 1$，
把点C(-1,a)代入$y=-x + 1$中，得$a=1 + 1=2$，
∴点C的坐标为(-1,2)。(2分)
把C(-1,2)代入$y=\frac{m}{x}$中，得$2=\frac{m}{-1}$，$m=-2$，(3分)
∴反比例函数解析式为$y=-\frac{2}{x}$（或写成$y=\frac{-2}{x}$）。(4分)
(2)如图，过C点作CH⊥y轴于点H。
∵C(-1,2)，
∴CH=1。 (5分)
把$x = 0$代入$y=-x + 1$得，$y = 1$。
∴B(0,1)，
∴OB=1， (6分)
∴$S_{\triangle BOC}=\frac{1}{2}OB· CH=\frac{1}{2}×1×1=\frac{1}{2}$。(7分)

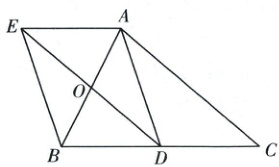
20. （7 分）如图，在 $\triangle ABC$ 中，点 $O$，$D$ 分别是边 $AB$，$BC$ 的中点，过点 $A$ 作 $AE// BC$ 交 $DO$ 的延长线于点 $E$，连接 $AD$，$BE$.
(1) 求证：四边形 $AEBD$ 是平行四边形；
(2) 若 $AB = AC$，试判断四边形 $AEBD$ 的形状，并证明.

答案：
(1)证明：
∵点O为AB的中点，
∴OA=OB。 (1分)
∵AE//BC，
∴∠EAO=∠OBD，∠AEO=∠BDO。
在△AEO和△BDO中，
$\begin{cases}∠EAO = ∠OBD, \\ ∠AEO = ∠BDO, \\ OA = OB,\end{cases}$
∴△AEO≌△BDO(AAS) (3分)
∴AE=BD。
∵AE//BD，
∴四边形AEBD是平行四边形。 (4分)
(2)当AB=AC时，四边形AEBD是矩形。
证明如下：
∵AB=AC，点D是BC边上的中点，
∴AD⊥BC即∠ADB=90°。 (6分)
由
(1)得四边形AEBD是平行四边形，
∴四边形AEBD是矩形。 (7分)

21. (6 分)数学实践
【问题背景】

中国传统农业智慧遇上现代数学模型. “豇豆不上架，产量少一半”的农谚流传至今，现代科学揭示了其秘密：当支架与地面形成 $65^{\circ}$ 夹角时，既能在早春聚热防冻害，又能在盛夏分散强光，就像给豇豆装了智能遮阳篷.
【问题呈现】
用两根竹竿交叉，斜插入地面，交叉点在何处会使支架与地面形成 $65^{\circ}$ 夹角？
【模型建立】
环节一：数据收集
两根竹竿长度均为 1.8 米，插入地下的部分为 0.3 米，竹竿与地面接触点间距为 0.6 米，且与地面所形成的夹角均为 65°.
环节二：数学抽象
如图：已知线段 $AB$ 与 $CD$ 交于点 $O$，$AB$，$CD$ 与直线 $l$ 分别交于点 $E$，$F$，$AB = CD = 1.8$ m，$BE = DF = 0.3$ m，$∠AEF = ∠CFE = 65^{\circ}$，$EF = 0.6$ m，求 $OE$ 的长度.(结果精确到 0.1，参考数据：$\sin 65^{\circ}\approx 0.91$，$\cos 65^{\circ}\approx 0.42$，$\tan 65^{\circ}\approx 2.14$)

【模型求解】
【问题总结】
交叉点 $O$ 距顶端 $A$ 的长度 $OA$ 为0.8m 时，支架与地面形成 $65^{\circ}$ 夹角，这样更贴合作物的生长规律.

答案：
【模型求解】如图，过O点作OH⊥EF，垂足为H。 (1分)
∵∠AEF=∠CFE=65°，
∴OE=OF，

∴$EH=\frac{1}{2}EF = 0.3$m。 (3分)
在Rt△OEH中，∠OEF=65°，
$\cos65°=\frac{EH}{OE}=\frac{0.3}{OE}$，
∴$OE=\frac{0.3}{\cos65°}\approx\frac{0.3}{0.42}\approx0.7$m， (5分)
【问题总结】0.8 (6分)