《2025年金考卷中考45套汇编数学》

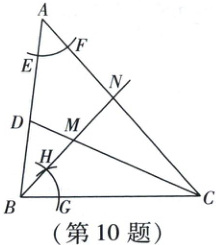
10. 如图，$CD$是$\triangle ABC$的角平分线。按以下步骤作图：①以点$A$为圆心，适当长为半径画弧，与边$AB$相交于点$E$，与边$AC$相交于点$F$；②以点$B$圆心，$AE$长为半径画弧，与边$BC$相交于点$G$；③以点$G$圆心，$EF$长为半径画弧，与第②步中所画的弧相交于点$H$；④作射线$BH$，与$CD$相交于点$M$，与边$AC$相交于点$N$。则下列结论一定正确的是(D)

A.$\angle ABN=\angle A$
B.$BN\perp AC$
C.$CM=AD$
D.$BM=BD$

答案： 10 D 逐项分析如下, 故选D.
选项 分析 是否符合题意
A 反例验证: 假设 ∠ABC = 80°, AB = CB, 则 ∠A = $\frac{1}{2} × (180° - 80°)$ = 50°. 由作图知 ∠CBN = ∠A = 50°,
∴ ∠ABN = 30°,
∴ ∠ABN ≠ ∠A. 否
B 若 BN ⊥ AC, 则 ∠BCN + ∠NBC = 90°. 又 ∠A = ∠NBC,
∴ ∠BCN + ∠A = 90°, ∠ABC = 90°. 而 ∠ABC 不一定等于 90°,
∴ BN 不一定垂直于 AC. 否
C 反例验证: 假设 ∠ABC = 90°, ∠A = 30°, ∠ACB = 60°, BC = 1, 则 AB = $\sqrt{3} BC = \sqrt{3}$.
∵ CD 平分 ∠ACB,
∴ ∠BCD = $\frac{1}{2} ∠ACB$ = 30°,
∴ BD = $\frac{\sqrt{3}}{3} BC = \frac{\sqrt{3}}{3}$,
∴ AD = AB - BD = $\sqrt{3} - \frac{\sqrt{3}}{3} = \frac{2}{3} \sqrt{3}$. 易知 BM = CM, 过点 M 作 MQ ⊥ BC 于点 Q, 则 CQ = $\frac{1}{2} BC = \frac{1}{2}$,
∴ CM = $\frac{\sqrt{3}}{3}$,
∴ CM ≠ AD. 否
D 由作图可知 ∠CAD = ∠CBM.
∵ CD 平分 ∠ACB,
∴ ∠ACD = ∠BCD,
∴ ∠ADC = ∠BMC,
∴ ∠BDM = ∠BMD,
∴ BM = BD. 是

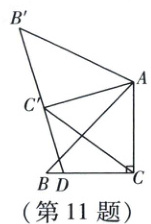
11. 如图，在$\triangle ABC$中，$\angle ACB=90^{\circ}$，将$\triangle ABC$绕点$A$顺时针旋转得到$\triangle AB'C'$，点$B$，$C$的对应点分别为$B'$，$C'$，$B'C'$的延长线与边$BC$相交于点$D$，连接$CC'$。若$AC=4$，$CD=3$，则线段$CC'$的长为(D)

A.$\frac{12}{5}$
B.$\frac{16}{5}$
C.4
D.$\frac{24}{5}$

答案：
11 D 如图, 连接 AD, 设 AD 交 CC' 于点 O. 由旋转可知 AC' = AC = 4, ∠AC'B' = ∠ACB = 90°,
∴ ∠AC'D = 90°, ∠AC'D = ∠ACB = 90°. 又
∵ AD = AD,
∴ Rt △ACD ≌ Rt △AC'D (HL),
∴ C'D = CD = 3,
∴ AD 垂直平分 CC' (点拨: 到线段两端点的距离相等的点, 在这条线段的垂直平分线上),
∴ CC' = 2CO. 易知 AD = $\sqrt{CD^2 + AC^2} = \sqrt{3^2 + 4^2} = 5$.
∵ S_△ACD = $\frac{1}{2} CD · AC = \frac{1}{2} AD · CO$,
∴ 3 × 4 = 5CO,
∴ CO = $\frac{12}{5}$,
∴ CC' = 2CO = $\frac{24}{5}$.

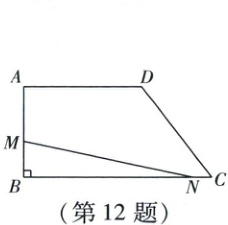
12. 四边形$ABCD$中，$AD// BC$，$\angle B=90^{\circ}$，$AB=8\ cm$，$AD=10\ cm$，$BC=16\ cm$。动点$M$从点$B$出发，以$2\ cm/s$的速度沿边$BA$、$AD$向终点$D$运动；动点$N$从点$C$同时出发，以$1\ cm/s$的速度沿边$CB$向终点$B$运动。规定其中一个动点到达终点时，另一个动点也随之停止运动。设运动的时间为$t\ s$。当$t=2$时，点$M$，$N$的位置如图所示。有下列结论：
①当$t=6$时，$CN=DM$；②当$1\leqslant t\leqslant 2$时，$\triangle BMN$的最大面积为$26\ cm^{2}$；
③$t$有两个不同的值满足$\triangle BMN$的面积为$39\ cm^{2}$。
其中，正确结论的个数是(C)

A.0
B.1
C.2
D.3

答案： 12 C 逐个分析如下, 故选C.
结论 分析 正误
当 t = 6 时, 点 M 的运动路程为 6 × 2 = 12 (cm), 点 N 的运动路程为 6 × 1 = 6(cm), 此时点 M 在 AD 上, 如图所示, DM = AB + AD - (AB + AM) = 8 + 10 - 12 = 6(cm),
∴ CN = DM. √
当 1 ≤ t ≤ 2 时, 点 M 在 AB 上.
∵ BM = 2t cm, CN = t cm,
∴ BN = (16 - t) cm,
∴ S_△BMN = $\frac{1}{2} BN · BM = \frac{1}{2} (16 - t) · 2t = - (t - 8)^2 + 64$,
∴ 当 t = 2 时, S_△BMN 取得最大值, 最大值为 28 cm². ✕
当 0 ≤ t ≤ 4, 即点 M 在 AB 上时, S_△BMN = $\frac{1}{2} BN · BM = \frac{1}{2} (16 - t) · 2t = - (t - 8)^2 + 64$, 令 - (t - 8)^2 + 64 = 39, 解得 t₁ = 3, t₂ = 13 (舍去). 当 4 ＜ t ≤ 9, 即点 M 在 AD 上时, S_△BMN = $\frac{1}{2} BN · AB = \frac{1}{2} (16 - t) · 8 = -4t + 64$, 令 -4t + 64 = 39, 解得 t = 6.25. 综上可知, t 有两个不同的值满足 △BMN 的面积为 39 cm². √

13. 不透明袋子中装有13个球，其中有3个红球、4个黄球、6个绿球，这些球除颜色外无其他差别。从袋子中随机取出1个球，则它是绿球的概率为$\frac{6}{13}$。

答案： 13 $\frac{6}{13}$

14. 计算$3x-x-5x$的结果为-3x。

答案： 14 -3x

15. 计算$(\sqrt{61}+1)× (\sqrt{61}-1)$的结果为60。

答案： 15 60

16. 将直线$y=3x-1$向上平移$m$个单位长度，若平移后的直线经过第三、第二、第一象限，则$m$的值可以是2(写出

一

个

即可)。

答案： 16 2 (答案不唯一, 满足 m ＞ 1 即可)

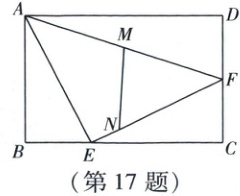
17. 如图，在矩形$ABCD$中，$AB=2$，$BC=3$，点$E$在边$BC$上，且$EC=2BE$。
(Ⅰ)线段$AE$的长为$\sqrt{5}$；
(Ⅱ)$F$为$CD$的中点，$M$为$AF$的中点，$N$为$EF$上一点，若$\angle FMN=75^{\circ}$，则线段$MN$的长为$\frac{\sqrt{15}}{3}$。

答案：
17 (I) $\sqrt{5}$ (II) $\frac{\sqrt{15}}{3}$
【解析】(I) 由 BC = 3, EC = 2BE 可知, BE = 1, EC = 2,
∴ AE = $\sqrt{AB^2 + BE^2} = \sqrt{2^2 + 1^2} = \sqrt{5}$. (II)
∵ F 为 CD 的中点, CD = AB = 2,
∴ CF = DF = $\frac{1}{2} CD = 1$,
∴ AF = $\sqrt{AD^2 + DF^2} = \sqrt{3^2 + 1^2} = \sqrt{10}$, EF = $\sqrt{EC^2 + CF^2} = \sqrt{2^2 + 1^2} = \sqrt{5}$.
∵ ($\sqrt{5}$)² + ($\sqrt{5}$)² = ($\sqrt{10}$)², 即 AE² + EF² = AF²,
∴ ∠AEF = 90° (依据: 勾股定理的逆定理). 又
∵ AE = EF,
∴ ∠EAF = 45°. 如图, 过点 M 作 MH // AE 交 EF 于点 H, 则 ∠MHF = ∠AEF = 90°,
∴ ∠FMH = ∠FMN - ∠FMH = 30°. 易知 MH 为 △AEF 的中位线,
∴ MH = $\frac{1}{2} AE = \frac{\sqrt{5}}{2}$ (依据: 三角形中位线定理),
∴ MN = $\frac{MH}{\cos 30°} = \frac{\frac{\sqrt{5}}{2}}{\frac{\sqrt{3}}{2}} = \frac{\sqrt{15}}{3}$.

18. 如图，在每个小正方形的边长为1的网格中，点$P$，$A$均在格点上。
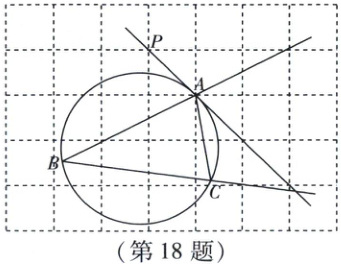
(Ⅰ)线段$PA$的长为$\sqrt{2}$。
（Ⅱ）直线$PA$与$\triangle ABC$的外接圆相切于点$A$，$AB=BC$。点$M$在射线$BC$上，点$N$在线段$BA$的延长线上，满足$CM=2AN$，且$MN$与射线$BA$垂直。请用

无

刻

度

的直尺，在如图所示的网格中，画出点$M$，$N$，并简要说明点$M$，$N$的位置是如何找到的（不要求证明）：如图(1), 直线 PA 与射线 BC 的交点为 M; 取圆与网格线的交点 D 和 E, 连接 DE; 取格点 F, 连接 AF, 与 DE 相交于点 O; 连接 BO 并延长, 与 AC 相交于点 G, 与直线 PA 相交于点 H; 连接 CH 并延长, 与网格线相交于点 I, 连接 AI, 与网格线相交于点 J; 连接 GJ, 与线段 BA 的延长线相交于点 N, 则点 M, N 即为所求.。

答案：
18 (I) $\sqrt{2}$ (II) 如图
(1), 直线 PA 与射线 BC 的交点为 M; 取圆与网格线的交点 D 和 E, 连接 DE; 取格点 F, 连接 AF, 与 DE 相交于点 O; 连接 BO 并延长, 与 AC 相交于点 G, 与直线 PA 相交于点 H; 连接 CH 并延长, 与网格线相交于点 I, 连接 AI, 与网格线相交于点 J; 连接 GJ, 与线段 BA 的延长线相交于点 N, 则点 M, N 即为所求.

名师教解题
本题的关键是确定点 M 的位置, 下面是确定点 M 位置的思路过程.
第一步: 如图
(1), 在此题中先确定 ∠BAC = ∠QAR.
易知 ∠K + ∠BAK = 90°, ∠PAB + ∠BAK = 90°,
∴ ∠K = ∠PAB.
∵ BA = BC,
∴ ∠BAC = ∠C. 又
∵ ∠K = ∠C,
∴ ∠BAC = ∠PAB. 又 ∠PAB = ∠QAR,
∴ ∠BAC = ∠QAR.

第二步: 确定点 M 的位置.
如图
(2), 在 BC 的延长线上取点 M, 在 BA 的延长线上取点 N. 由 CM = 2AN, 可想到在点 N 右侧取点 M', 使得 NM' = AN, 则 AM' = CM.
∵ MN ⊥ AN, NM' = AN,
∴ AM = M'M,
∴ ∠M'AM = ∠AM'M. 易证 AC // M'M,
∴ ∠BAC = ∠AM'M,
∴ ∠BAC = ∠M'AM. 易证点 M 在直线 PA 上. 又
∵ 点 M 在射线 BC 上,
∴ 点 M 是直线 PA 与射线 BC 的交点.