2025年金考卷中考45套汇编数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年金考卷中考45套汇编数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第15页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
17. 求不等式组:$\begin{cases}2x - 2\lt x,①\frac{x - 1}{2}\leq\frac{2x - 1}{3}②\end{cases}$的所有整数解。
答案:
17 解不等式①,得$x<2$.
解不等式②,得$x\geq-1$.
∴不等式组的解集为$-1\leq x<2$,
(5分)
∴该不等式组的所有整数解是$-1,0,1$.
(8分)
解不等式②,得$x\geq-1$.
∴不等式组的解集为$-1\leq x<2$,
(5分)
∴该不等式组的所有整数解是$-1,0,1$.
(8分)
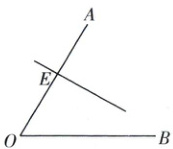
18. 学习了角平分线和尺规作图后,小红进行了拓展性研究,她发现了角平分线的另一种作法,并与她的同伴进行交流。现在你作为她的同伴,请根据她的想法与思路,完成以下作图和填空。
第一步:构造角平分线。
小红在$\angle AOB$的边$OA$上任取一点$E$,并过点$E$作了$OA$的垂线(如图)。请你利用尺规作图,在$OB$边上截取$OF = OE$,过点$F$作$OB$的垂线与小红所作的垂线交于点$P$,作射线$OP$,$OP$即为$\angle AOB$的平分线(不写作法,保留作图痕迹)。
第二步:利用三角形全等证明她的猜想。
证明:$\because PE\perp OA$,$PF\perp OB$,
$\therefore\angle OEP=\angle OFP = 90^{\circ}$。
在$\mathrm{Rt}\triangle OEP$和$\mathrm{Rt}\triangle OFP$中,
$\begin{cases}① $_________$ ,\\② $_________$ ,\end{cases}$
$\therefore\mathrm{Rt}\triangle OEP\cong\mathrm{Rt}\triangle OFP(\mathrm{HL})$,
$\therefore③$
$\therefore OP$平分$\angle AOB$。
第一步:构造角平分线。
小红在$\angle AOB$的边$OA$上任取一点$E$,并过点$E$作了$OA$的垂线(如图)。请你利用尺规作图,在$OB$边上截取$OF = OE$,过点$F$作$OB$的垂线与小红所作的垂线交于点$P$,作射线$OP$,$OP$即为$\angle AOB$的平分线(不写作法,保留作图痕迹)。

第二步:利用三角形全等证明她的猜想。
证明:$\because PE\perp OA$,$PF\perp OB$,
$\therefore\angle OEP=\angle OFP = 90^{\circ}$。
在$\mathrm{Rt}\triangle OEP$和$\mathrm{Rt}\triangle OFP$中,
$\begin{cases}① $_________$ ,\\② $_________$ ,\end{cases}$
$\therefore\mathrm{Rt}\triangle OEP\cong\mathrm{Rt}\triangle OFP(\mathrm{HL})$,
$\therefore③$
$\angle EOP=\angle FOP$
,$\therefore OP$平分$\angle AOB$。
答案:
18 第一步:作图如图所示.
(4分)
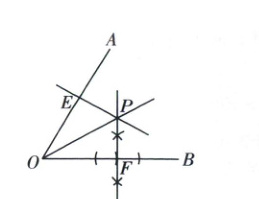
第二步:①$PO=PO$ ②$OE=OF$(或①$OE=OF$ ②$PO=PO$)
(6分)
③$\angle EOP=\angle FOP$(或$\angle FOP=\angle EOP$)
(8分)

18 第一步:作图如图所示.
(4分)

第二步:①$PO=PO$ ②$OE=OF$(或①$OE=OF$ ②$PO=PO$)
(6分)
③$\angle EOP=\angle FOP$(或$\angle FOP=\angle EOP$)
(8分)

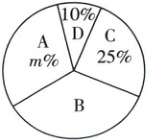
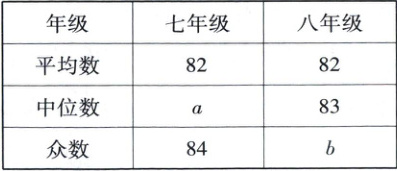
19. 学校开展了航天知识竞赛活动,从七、八年级学生中各随机抽取20名学生的竞赛成绩(成绩为百分制且为整数)进行整理、描述和分析(成绩均不低于60分,用$x$表示,共分四组:$A.90\leq x\lt100$;$B.80\leq x\lt90$;$C.70\leq x\lt80$;$D.60\leq x\lt70$),下面给出了部分信息:
七年级20名学生竞赛成绩在$B$组中的数据是83,84,84,84,85,87,88。
八年级20名学生竞赛成绩是62,63,65,71,72,72,75,78,81,82,84,86,86,89,96,97,98,98,99。
七年级所抽取学生竞赛成绩扇形统计图
七、八年级所抽取学生竞赛成绩统计表
根据以上信息,解答下列问题:
(1)上述图表中$a=$
(2)根据以上数据,你认为该校七、八年级中哪个年级学生航天知识竞赛的成绩较好?请说明理由(写出一条理由即可)。
(3)该校七年级有学生560人,八年级有学生500人,请估计该校七、八年级参加此次竞赛成绩不低于90分的学生人数共是多少。
七年级20名学生竞赛成绩在$B$组中的数据是83,84,84,84,85,87,88。
八年级20名学生竞赛成绩是62,63,65,71,72,72,75,78,81,82,84,86,86,89,96,97,98,98,99。
七年级所抽取学生竞赛成绩扇形统计图
七、八年级所抽取学生竞赛成绩统计表


根据以上信息,解答下列问题:
(1)上述图表中$a=$
84.5
,$b=$86
,$m=$30
。(2)根据以上数据,你认为该校七、八年级中哪个年级学生航天知识竞赛的成绩较好?请说明理由(写出一条理由即可)。
(3)该校七年级有学生560人,八年级有学生500人,请估计该校七、八年级参加此次竞赛成绩不低于90分的学生人数共是多少。
答案:
19
(1)84.5 86 30
(6分)
解法提示:七年级20名学生竞赛成绩在D组中的数据有
$20×10\%=2$(人),在C组中的数据有$20×25\%=5$(人).
∵七年级竞赛成绩的数据从小到大排列后的第10和11个
数据是84,85,
∴$a=\frac{84+85}{2}=84.5$.
∵八年级20名学生竞赛成绩的数据中出现次数最多的是
86,
∴$b=86$.
∵七年级20名学生竞赛成绩在B组中的数据共7个,
∴$m\%=1-10\%-25\%-\frac{7}{20}=30\%$,
∴$m=30$.
(2)答案一:该校七年级学生航天知识竞赛的成绩较好.
(7分)
理由:因为该校七、八年级学生航天知识竞赛成绩的平均数
都是82,但七年级竞赛成绩的中位数84.5大于八年级竞赛
成绩的中位数83,所以该校七年级学生航天知识竞赛成绩
较好.
(8分)
答案二:该校八年级学生航天知识竞赛的成绩较好.(7分)
理由:因为该校七、八年级学生航天知识竞赛成绩的平均数
都是82,但八年级竞赛成绩的众数86大于七年级竞赛成绩
的众数84,所以该校八年级学生航天知识竞赛成绩较好.
(8分)
(3)$560×30\%+500×\frac{5}{20}=293$.
答:估计该校七、八年级参加此次竞赛成绩不低于90分的
学生人数共是293.
(10分)
(1)84.5 86 30
(6分)
解法提示:七年级20名学生竞赛成绩在D组中的数据有
$20×10\%=2$(人),在C组中的数据有$20×25\%=5$(人).
∵七年级竞赛成绩的数据从小到大排列后的第10和11个
数据是84,85,
∴$a=\frac{84+85}{2}=84.5$.
∵八年级20名学生竞赛成绩的数据中出现次数最多的是
86,
∴$b=86$.
∵七年级20名学生竞赛成绩在B组中的数据共7个,
∴$m\%=1-10\%-25\%-\frac{7}{20}=30\%$,
∴$m=30$.
(2)答案一:该校七年级学生航天知识竞赛的成绩较好.
(7分)
理由:因为该校七、八年级学生航天知识竞赛成绩的平均数
都是82,但七年级竞赛成绩的中位数84.5大于八年级竞赛
成绩的中位数83,所以该校七年级学生航天知识竞赛成绩
较好.
(8分)
答案二:该校八年级学生航天知识竞赛的成绩较好.(7分)
理由:因为该校七、八年级学生航天知识竞赛成绩的平均数
都是82,但八年级竞赛成绩的众数86大于七年级竞赛成绩
的众数84,所以该校八年级学生航天知识竞赛成绩较好.
(8分)
(3)$560×30\%+500×\frac{5}{20}=293$.
答:估计该校七、八年级参加此次竞赛成绩不低于90分的
学生人数共是293.
(10分)
查看更多完整答案,请扫码查看


