《2025年金考卷中考45套汇编数学》

14. 现有六张分别标有数字1，2，3，4，5，6的卡片，其中标有数字1，4，5的卡片在甲手中，标有数字2，3，6的卡片在乙手中. 两人各随机出一张卡片，甲出的卡片数字比乙大的概率是4/9.

答案：
14 4/9
[解析]画树状图如图所示，可知共有9种等可能的情况，其中甲出的卡片数字比乙大的情况有4种，故所求概率为4/9.

15. 新课标 数学文化 【文化欣赏】
我国南宋时期数学家杨辉于1261年写下《详解九章算法》，书中记载的二项和的乘方 $(a + b)^{n}$ 展开式的系数规律如图所示，其中“三乘”对应的展开式如下：
$(a + b)^{4} = a^{4} + 4a^{3}b + 6a^{2}b^{2} + 4ab^{3} + b^{4}$.
【应用体验】
已知 $(x + 2)^{4} = x^{4} + mx^{3} + 24x^{2} + 32x + 16$，则 $m$ 的值为8.

答案： 15 8
[解析]将(x + 2)⁴套用(a + b)⁴的展开式，可知a = x，b = 2，对照两式的展开式，可得4a³b = mx³，
∴m = 4b = 8.

16. 如图，矩形 $ABCD$ 内接于 $\odot O$，$E$ 是 $\overset{\frown}{AD}$ 上一点，连接 $EB$，$EC$ 分别交 $AD$ 于点 $F$，$G$. 若 $AF = 1$，$EG = FG = 3$，则 $\odot O$ 的直径为2√14.

答案：
16 2√14
[解析]如图，连接AE.
∵AF = 1，FG = 3，
∴AG = AF + FG = 4.
∵AC是⊙O的直径，
∴∠AEC = 90°(依据：直径所对的圆周角为90°)，
∴AE = √AG² - EG² = √4² - 3² = √7.
∵EG = FG，
∴∠GEF = ∠GFE.
∵AD//BC，
∴∠GFE = ∠CBE，
∴∠CBE = ∠GEF，
∴CE = CB = AD.又
∵AC = CA，
∴Rt△ADC≅Rt△CEA(HL)，
∴CD = AE = √7.又
∵∠AEG = ∠D = 90°，∠AGE = ∠CGD，
∴△AEG≅△CDG(AAS)，
∴GD = EG = 3，
∴AD = AG + GD = 4 + 3 = 7，
∴AC = √AD² + CD² = √7² + (√7)² = 2√14.
巧作辅助线：直径、直角互相关联

17. （本题8分）化简求值：$x(5 - x) + x^{2} + 3$，其中 $x = 2$.

答案： 17 原式 = 5x - x² + x² + 3 = 5x + 3. (4分)
当x = 2时，原式 = 5×2 + 3 = 13. (8分)

18. （本题8分）解分式方程：$\frac{3}{x + 1} - \frac{1}{x - 1} = 0$.

答案： 18 方程两边同乘(x + 1)(x - 1)，得3(x - 1) - (x + 1) = 0. (4分)
解得x = 2.
检验：把x = 2代入原方程，得左边 = 3/(2 + 1) - 1/(2 - 1) = 0 = 右边，当x = 2时，(x + 1)(x - 1) = 3×1≠0，因此x = 2是原分式方程的解. (8分)

19. （本题8分）
【问题背景】
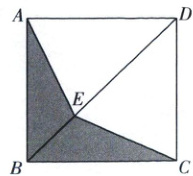
如图所示，某兴趣小组需要在正方形纸板 $ABCD$ 上剪下机翼状纸板（阴影部分），点 $E$ 在对角线 $BD$ 上.
【数学理解】
（1）该机翼状纸板是由两个全等三角形组成的，请写出 $\triangle ABE \cong \triangle CBE$ 的证明过程.
（2）若裁剪过程中满足 $DE = DA$，求“机翼角” $\angle BAE$ 的度数.

答案： 19
(1)证明：在正方形ABCD中，BA = BC，∠ABD = ∠CBD = 45°.
在△ABE和△CBE中，{BA = BC，∠ABE = ∠CBE，BE = BE}，所以△ABE≅△CBE(SAS). (4分)
(2)在正方形ABCD中，∠BAD = 90°，∠ADB = 45°.
因为DE = DA，所以∠DAE = ∠DEA = 67.5°，所以∠BAE = 90° - 67.5° = 22.5°. (8分)