《2025年金考卷中考45套汇编数学》

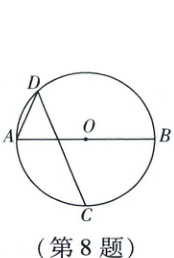
8. 如图，AB为$\odot O$的直径，点C，D是$\odot O$上位于AB异侧的两点，连接AD，CD。若$\widehat{AC} = \widehat{BC}$，则$\angle D$的度数为(B)

A.$30^{\circ}$
B.$45^{\circ}$
C.$60^{\circ}$
D.$75^{\circ}$

答案：
8 B 如图,连接$AC$,$BC$. $\because AB$是$\odot O$的直径, $\therefore \angle ACB = 90^{\circ}$(依据：直径所对的圆周角是直角). $\because AC = BC$, $\therefore \angle CAB = \angle CBA = \frac{180^{\circ} - \angle ACB}{2} = 45^{\circ}$, $\therefore \angle ABC = \angle D = 45^{\circ}$(依据：同弧所对的圆周角相等).故选B.

一题多解
如图,连接$CO$. $\because AC = BC$, $\therefore \angle AOC = \angle BOC = \frac{\angle AOB}{2} = 90^{\circ}$, $\therefore \angle ADC = \frac{\angle AOC}{2} = 45^{\circ}$(依据：圆周角定理).故选B.

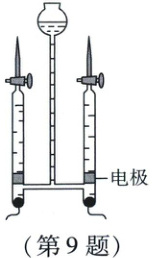
9. 新课标 跨学科试题 氢气是一种绿色清洁能源，可通过电解水获得，如图。实践小组通过实验发现，在电解水的过程中，生成物氢气的质量$y(g)$与分解的水的质量$x(g)$满足我们学过的某种函数关系。下表是一组实验数据，根据表中数据，$y$与$x$之间的函数关系式为(C)


A.$y = \frac{9}{x}$
B.$y = 9x$
C.$y = \frac{1}{9}x$
D.$y = \frac{1}{9x}$

答案： 9 C 观察可知,$y$是$x$的一次函数,设$y = kx + b$,将$(9,1)$,$(18,2)$分别代入可知$y$关于$x$的函数关系式为$y = \frac{1}{9}x$.故选C.

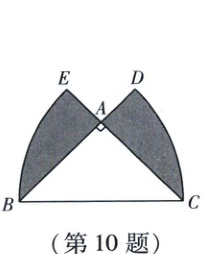
10. 如图，在$\triangle ABC$中，$\angle BAC = 90^{\circ}$，$AB = AC$，分别以点B，C为圆心、BC的长为半径画弧，与BA，CA的延长线分别交于点D，E。若$BC = 4$，则图中阴影部分的面积为(D)

A.$2\pi - 4$
B.$4\pi - 4$
C.$8\pi - 8$
D.$4\pi - 8$

答案： 10 D 快招解题法 试题秒解 考场速用
第一步：使用容斥原理法
$S_{阴影部分} = S_{扇形BCD} + S_{扇形CBE} - 2S_{\triangle ABC}$.
第二步：求涉及的扇形圆心角;求涉及的三角形的边长、高
在$\triangle ABC$中,$\angle BAC = 90^{\circ}$,$AB = AC$, $\therefore \angle ABC = \angle ACB = 45^{\circ}$,$\therefore AB = AC = \frac{\sqrt{2}}{2}BC = 2\sqrt{2}$.
第三步：求阴影部分的面积
$S_{阴影部分} = S_{扇形BCD} + S_{扇形CBE} - 2S_{\triangle ABC} = 2 × \frac{45}{360} \pi × 4^{2} - 2 × \frac{1}{2} × 2\sqrt{2} × 2\sqrt{2} = 4\pi - 8$.故选D.
更多讲解详见《解题有招》夹册“快招8”

11. 因式分解：$m^2 - 16 =$$(m+4)(m-4)$。

答案： 11 $(m + 4)(m - 4)$

12. 近年来，我省依托乡村e镇建设，打造农村电商新产业，提高了农民收入。某农户通过网上销售传统手工艺品布老虎(如图)，利润由原来的每个20元增加到80元。该农户通过网上售出$a$个布老虎，则他的利润增加了60a元(用含$a$的代数式表示)。

答案： 12 $60a$
【解析】方法一：“利润由原来的每个$20$元增加到$80$元”，则每个布老虎利润增加了$60$元，故通过网上售出$a$个布老虎后，利润增加了$60a$元。方法二：$80a - 20a = 60a$(元)，故通过网上售出$a$个布老虎后，利润增加了$60a$元。

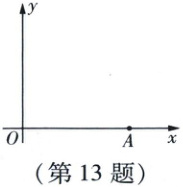
13. 如图，在平面直角坐标系中，点A的坐标为$(6,0)$，将线段OA绕点O逆时针旋转$45^{\circ}$，则点A对应点的坐标为$(3\sqrt{2},3\sqrt{2})$。

答案：
13 $(3\sqrt{2},3\sqrt{2})$
【解析】设点$A$旋转后的对应点为$A'$，则$\angle AOA' = 45^{\circ}$，$OA' = OA = 6$。如图，过点$A'$作$A'B \perp x$轴于点$B$，则$A'B = OA' · \sin 45^{\circ} = 3\sqrt{2}$，$OB = OA' · \cos 45^{\circ} = 3\sqrt{2}$，$\therefore A'(3\sqrt{2}, 3\sqrt{2})$，即点$A$对应点的坐标为$(3\sqrt{2}, 3\sqrt{2})$。

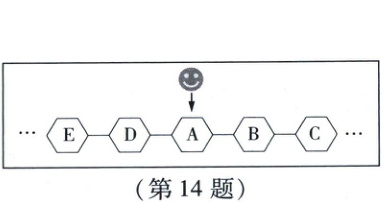
14. 新考法 结合程序考查概率 如图是创新小组设计的一款小程序的界面示意图，程序规则为：每点击一次按钮，“”就从一个格子向左或向右随机移动到相邻的一个格子。当“”位于格子A时，小明连续点击两次按钮，“”回到格子A的概率是$\frac{1}{2}$。

答案：
14 $\frac{1}{2}$
【解析】根据题意，画树状图如下。

由树状图可知，共有$4$种等可能的结果，其中“”回到格子$A$的结果有$2$种，故所求概率为$\frac{2}{4} = \frac{1}{2}$。

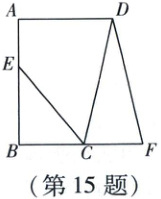
15. 如图，在四边形ABCD中，$AD // BC$，$\angle B = 90^{\circ}$，$AB = 8$，$BC = 4$，点E在边AB上，$AE = 3$，连接CE，且$\angle DCE = \angle BCE$。点F在BC的延长线上，连接DF。若$DF = DC$，则线段CF的长为$\frac{18}{5}$。

答案：
15 $\frac{18}{5}$
快招解题法 试题秒解 考场速用
本题可联想角平分线和平行产生等腰三角形进行求解，具体如下。
在$Rt \triangle BCE$中，$CE = \sqrt{BC^{2} + BE^{2}} = \sqrt{41}$，$\sin \angle ECB = \frac{5}{\sqrt{41}}$，$\cos \angle ECB = \frac{4}{\sqrt{41}}$。如图，分别延长$CE$，$DA$，两线交于点$Q$。$\because AD // BC$，$\therefore \angle QAE = \angle B = 90^{\circ}$，$\angle Q = \angle ECB$，$\sin Q = \frac{5}{\sqrt{41}}$，$\cos Q = \frac{4}{\sqrt{41}}$，$\therefore EQ = \frac{AE}{\sin Q} = \frac{3}{\frac{5}{\sqrt{41}}} = \frac{3\sqrt{41}}{5}$，$\therefore QC = EQ + EC = \frac{3\sqrt{41}}{5} + \sqrt{41} = \frac{8\sqrt{41}}{5}$。$\because \angle DCE = \angle BCE$，$\therefore \angle Q = \angle DCQ$，$\therefore DQ = DC$(点拨：角平分线+平行→等腰三角形)。过点$D$作$DG \perp QC$于点$G$，则$QG = GC = \frac{1}{2}QC = \frac{4\sqrt{41}}{5}$，$\therefore DC = \frac{GC}{\cos \angle DCG} = \frac{\frac{4\sqrt{41}}{5}}{\frac{4}{\sqrt{41}}} = \frac{41}{5}$。过点$D$作$DH \perp CF$于点$H$。$\because DC = DF$，$\therefore CH = FH$。易得四边形$ABHD$是矩形，$\therefore DH = AB = 8$，$\therefore CH = \sqrt{DC^{2} - DH^{2}} = \sqrt{(\frac{41}{5})^{2} - 8^{2}} = \frac{9}{5}$，$\therefore CF = 2CH = \frac{18}{5}$。
巧作辅助线：遇等腰三角形，想“三线合一”
点拨：角平分线+平行→等腰三角形
一题多解
方法一：如图
(1)，分别延长$CE$，$DA$，两线交于点$Q$。$\because AD // BC$，$\therefore \angle Q = \angle ECB$。又$\because \angle QEA = \angle CEB$，$\therefore \triangle EAQ \sim \triangle EBC$(点拨：“8”字型相似)，$\therefore \frac{AE}{BE} = \frac{AQ}{BC}$，$\therefore AQ = \frac{12}{5}$。$\because \angle DCE = \angle BCE$，$\therefore \angle Q = \angle DCE$，$\therefore DQ = DC$(点拨：角平分线+平行→等腰三角形)。过点$D$作$DH \perp CF$于点$H$，则四边形$ABHD$为矩形，$\therefore AD = BH = CH + 4$，$DH = AB = 8$。$\because DC = DF$，$\therefore CH = FH$。设$CH = HF = m$，则$DC = DF = DQ = m + 4 + \frac{12}{5} = m + \frac{32}{5}$。在$Rt \triangle DCH$中，$DC^{2} = DH^{2} + CH^{2}$，即$(m + \frac{32}{5})^{2} = 8^{2} + m^{2}$，解得$m = \frac{9}{5}$，$\therefore CF = 2m = \frac{18}{5}$。

方法二：如图
(2)，过点$D$作$DH \perp CF$于点$H$，则$CH = FH$。易证四边形$ABHD$是矩形，$\therefore DH = AB = 8$。过点$D$作$EC$的平行线交$BF$的延长线于点$J$，则$\angle CDJ = \angle DCE$，$\angle ECB = \angle CDJ = \angle J$，$\therefore CD = CJ$。在$Rt \triangle EBC$中，$EB = 5$，$BC = 4$，$\tan \angle ECB = \frac{5}{4}$，$\therefore \tan J = \frac{5}{4}$，$\therefore HJ = \frac{DH}{\tan J} = \frac{32}{5}$，$\therefore CD = CJ = CH + \frac{32}{5}$。设$CH = m$，在$Rt \triangle DCH$中，$DC^{2} = DH^{2} + CH^{2}$，即$(m + \frac{32}{5})^{2} = 8^{2} + m^{2}$，解得$m = \frac{9}{5}$，$\therefore CF = 2m = \frac{18}{5}$。

方法三：如图
(3)，过点$D$作$DH \perp CF$于点$H$，则$CH = FH$。易证四边形$ABHD$是矩形，则$DH = AB = 8$。在$Rt \triangle EBC$中，$\angle EBC = 90^{\circ}$，$EB = 5$，$BC = 4$，$EC = \sqrt{41}$。设点$M$为$EC$的中点，连接$BM$，则$BM = MC = \frac{\sqrt{41}}{2}$，$\therefore \angle MBC = \angle MCB$，$\angle BME = 2 \angle ECB$。过点$B$作$BN \perp EC$于点$N$，则$BN = \frac{BE · BC}{EC} = \frac{20\sqrt{41}}{41}$，$\therefore MN = \sqrt{BM^{2} - BN^{2}} = \frac{9\sqrt{41}}{82}$，$\therefore \tan \angle BMN = \frac{BN}{MN} = \frac{40}{9}$。$\because \angle DCH = 180^{\circ} - \angle BCE - \angle ECD = 180^{\circ} - 2 \angle BCE$，$\angle BMN = 180^{\circ} - \angle BME = 180^{\circ} - 2 \angle ECB$，$\therefore \angle BMN = \angle DCH$，$\therefore \tan \angle DCH = \frac{DH}{CH} = \frac{40}{9}$，$\therefore CH = \frac{9}{5}$，$\therefore CF = 2CH = \frac{18}{5}$。

点拨：利用斜边上的中线构造“二倍角”