《2025年名校课堂九年级物理全一册沪粤版》

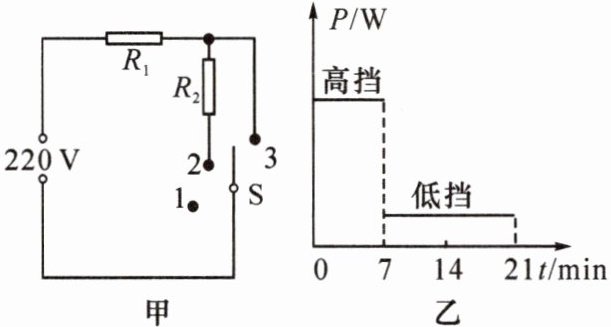
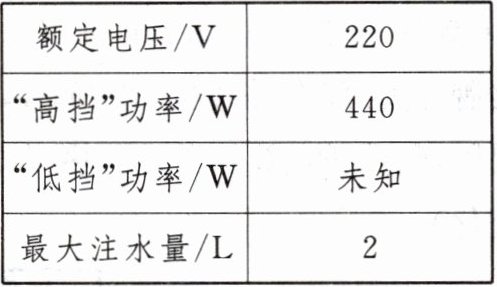
5. (2024·自贡)图甲是琪琪家某型号电热加湿器的电路图，如表所示为其部分技术参数。$ R_1 $、$ R_2 $ 为发热电阻，不考虑温度对电阻的影响，且 $ R_2 = 3R_1 $，$ S $ 为开关，1、2、3 为触点，通过旋转开关 $ S $ 可实现“关”“低挡”“高挡”之间的切换。
(1) 求电热加湿器处于“低挡”位置时的发热功率。
(2) 某次使用电热加湿器工作时，加湿器注水仓中加注冷水已达到最大注水量。图乙是使用电热加湿器工作 $ 21 \min $ 的 $ P - t $ 图像，如果“高挡”加热产生的热量全部被水吸收，则此次“高挡”加热可以使注水仓中冷水的温度升高多少？$ [\rho_{水} = 1.0 × 10^3 kg/m^3, c_{水} = 4.2 × 10^3 J/(kg·℃)] $

答案： 解:
(1)由图甲知，开关S接1触点时，电路开路，为“关”；接2触点时两电阻串联，为“低挡”；接3触点时只有$R_1$接入电路，为“高挡”。由$P=\frac{U^2}{R}$可得$R_1$的阻值：
　$R_1=\frac{U^2}{P_{高}}=\frac{(220V)^2}{440W}=110\Omega$
　$R_2$的阻值：
　$R_2=3R_1=3×110\Omega=330\Omega$
　则处于“低挡”位置时的发热功率：
　$P_{低}=\frac{U^2}{R_{总}}=\frac{U^2}{R_1+R_2}=\frac{(220V)^2}{110\Omega+330\Omega}=110W$
(2)由图乙可知，在“高挡”正常工作时消耗的电能：
　$W_{高}=P_{高}t_{高}=440W×7×60s=1.848×10^5J$
　电阻$R_1$产生的热量全部被水吸收，即
　$Q_{吸}=W_{高}=1.848×10^5J$
　注水仓中水的质量：
　$m=\rho_{水}V=1.0×10^3kg/m^3×2×10^{-3}m^3=2kg$
　由$Q_{吸}=cm\Delta t$可得，水升高的温度：
　$\Delta t=\frac{Q_{吸}}{c_{水}m}=\frac{1.848×10^5J}{4.2×10^3J/(kg·℃)×2kg}=22℃$