《2025年名校课堂八年级数学上册北师大版贵州专版》

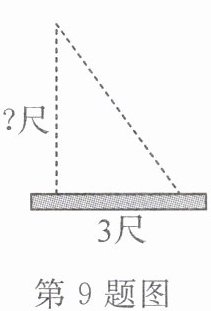
9. 新考向 数学文化《九章算术》中有一道题：“今有竹高一丈，末折抵地，去本三尺，问折者高几何?”大致意思：一根竹子高 1 丈，折断后竹子顶端落在离竹子底端 3 尺处，那么折断处离地面的高度为4.55尺.(1 丈 = 10 尺)

答案： 4.55

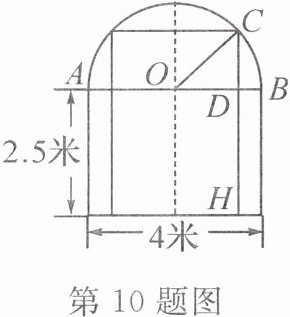
10. 北京四中校本经典题 一辆装满货物的卡车，其外形的宽为 2.4 米，高为 3.9 米，这辆卡车能(填“能”或“不能”)通过如图所示的隧道.

答案： 能

11. (2024·安顺期末)综合与实践
小明同学在延时课上进行了项目式学习实践探究，并绘制了如下记录表格：

请根据表格信息，解答下列问题.
(1)求线段 AD 的长.
(2)若想要风筝沿 DA 方向再上升 12 米，则在 ED 长度不变的前提下，小明同学应该再放出多少米风筝线?

答案： 解：
(1)过点B作BC⊥AD于点C.在Rt△ABC中，∠ACB=90°，BC=15米，AB=17米，由勾股定理，得$AC^{2}=AB^{2}-BC^{2}=17^{2}-15^{2}=64，$
∴AC=8米。
∴AD=AC+CD=8+1.6=9.6(米)。
(2)延长CA至点F，使AF=12米，连接BF.
∴CF=AC+AF=20米。由勾股定理，得$BF^{2}=CF^{2}+BC^{2}=20^{2}+15^{2}=625，$
∴BF=25米.此时风筝线的长为25米，25-17=8(米)。
答：小明同学应该再放出8米风筝线。

12. 兰生复旦校本经典题(2024·贵阳美的中学期中)台风是一种自然灾害，它以台风中心为圆心，在周围上千米的范围内形成极端气候，有极强的破坏力.如图，有一台风中心沿东西方向 AB 由点 A 向点 B 移动，点 C 为一海港，且点 C 与直线 AB 上两点 A，B 的距离分别为 300 km 和 400 km，$AB = 500\mathrm{km}$.已知以台风中心为圆心，周围 250 km 以内为受影响区域.
(1)海港 C 受台风影响吗? 为什么?
(2)若台风的移动速度为 20 km/h，则台风影响海港 C 的时间有多长?
]

答案： 解：
(1)海港C受台风影响.理由如下：过点C作CD⊥AB于点D.
∵AC=
300km，BC=400km，AB=500km，
∴$AC^{2}+BC^{2}=AB^{2}。$
∴△ABC是直角三角形，∠ACB=90°。
∴$S_{△ABC}=\frac{1}{2}AC·BC=\frac{1}{2}CD·AB。$
∴CD=
$\frac{AC·BC}{AB}=\frac{300×400}{500}=240(km)。$
∵240＜250，
∴海港C受台风影响。
(2)在直线AB上取点E，F，使EC=FC=250km，此时刚好影响海港C.由勾股定理，得$ED^{2}=EC^{2}-CD^{2}=4900，$
∴ED=70km.同理可得DF=70km，
∴EF=140km.
∴140÷20=7(h)。答：台风影响海港C的时间为7h。