《2025年名校课堂八年级数学上册北师大版贵州专版》

1. (2024·贵州改编)为增强学生的劳动意识，养成劳动的习惯和品质，某校组织学生参加劳动实践.经学校与劳动基地联系，计划组织学生参加种植甲、乙两种作物.如果种植 3 公顷甲作物和 2 公顷乙作物需要 405 名学生，种植 2 公顷甲作物和 2 公顷乙作物需要 330 名学生，那么种植 1 公顷甲作物和 1 公顷乙作物分别需要多少名学生？

答案： 解：设种植1公顷甲作物需要$x$名学生，种植1公顷乙作物需要$y$名学生.根据题意，得$\begin{cases}3x + 2y = 405,\\2x + 2y = 330,\end{cases}$解得$\begin{cases}x = 75,\\y = 90.\end{cases}$答：种植1公顷甲作物需要75名学生，种植1公顷乙作物需要90名学生.

2. 甲、乙两城相距 1120 千米，一列快车从甲城出发开往乙城，行驶 120 千米后，另一列动车从乙城出发开往甲城，2 个小时后两车相遇.若快车平均每小时行驶的路程比动车平均每小时行驶的路程的一半还多 5 千米，动车与快车平均每小时各行驶多少千米？

答案： 解：设动车平均每小时行驶$x$千米，快车平均每小时行驶$y$千米.依题意，得$\begin{cases}y = \frac{1}{2}x + 5,\\2(x + y) + 120 = 1120,\end{cases}$解得$\begin{cases}x = 330,\\y = 170.\end{cases}$答：动车平均每小时行驶330千米，快车平均每小时行驶170千米.

3. 新考向 开放性问题(2023·毕节金沙四中月考)为打造南渡江南侧风光带，现有一段长 350 米的河边道路整治任务由 A，B 两个工程队先后接力完成.A 工程队每天整治 15 米，B 工程队每天整治 10 米，共用时 30 天.
(1)根据题意，甲、乙两位同学分别列出了如下不完整的方程组：
甲：$\begin{cases}x + y = □,\\15x + 10y = □.\end{cases}$ 乙：$\begin{cases}x + y = □,\frac{x}{15} + \frac{y}{10} = □.\end{cases}$
根据甲、乙两位同学所列的方程组，请分别指出其中未知数 $x$ 表示的意义：
甲：$x$ 表示A工程队工作的天数.
乙：$x$ 表示A工程队整治的河边道路总长度.
(2)从甲、乙两位同学所列方程组中任选一组，将其补全，并利用此方程组求出 A，B 两个工程队分别整治河边道路多少米.

答案： 解：
(1)A工程队工作的天数 A工程队整治的河边道路总长度
(2)①若补全甲的方程组：$\begin{cases}x + y = 30,\\15x + 10y = 350,\end{cases}$解得$\begin{cases}x = 10,\\\therefore 15x = 150,10y = 200.\end{cases}$答：A，B两个工程队分别整治河边道路150米和200米.②若补全乙的方程组：$\begin{cases}x + y = 350,\frac{x}{15} + \frac{y}{10} = 30,\end{cases}$解得$\begin{cases}x = 150,\\y = 200.\end{cases}$答：A，B两个工程队分别整治河边道路150米和200米.

4. 为了鼓励市民节约用水，某市居民生活用水按阶梯式水价计费.下表是该市居民“一户一表”生活用水阶梯式计费价格表的一部分(水价计费=自来水费用+污水处理费用)：

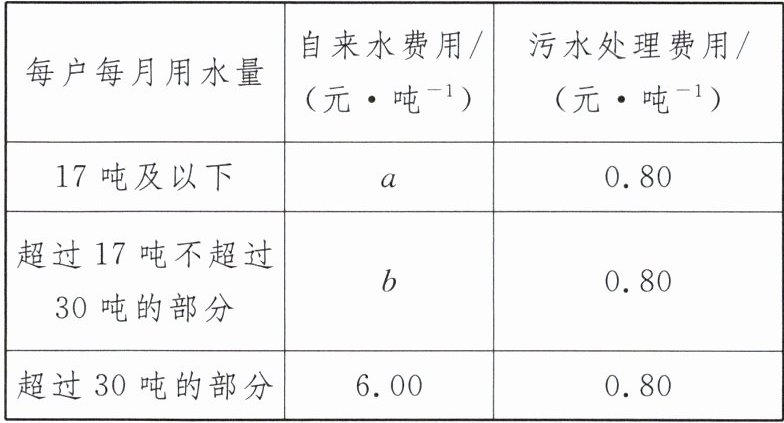
已知小王家 4 月份用水 20 吨，交水费 66 元；5 月份用水 25 吨，交水费 91 元.
(1)求 $a$，$b$ 的值.
(2)小王家 6 月份交水费 184 元，则小王家 6 月份用水多少吨？

答案： 解：
(1)根据题意，得$\begin{cases}17a + (20 - 17)b + 20 × 0.8 = 66,\\17a + (25 - 17)b + 25 × 0.8 = 91,\end{cases}$解得$\begin{cases}a = 2.2,\\b = 4.2.\end{cases}$
(2)$30$吨的水费为$17×2.2 + 13×4.2 + 30×0.8 = 116(元)$. $\because 184 ＞ 116$，$\therefore$小王家6月份用水量超过了30吨.设小王家6月份用水$x$吨.根据题意，得$116 + 6(x - 30) + 0.8(x - 30) = 184$，解得$x = 40$.答：小王家6月份用水40吨.