第15页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
11. (2024·贵阳期中)如图,有一个绳索被拉直的木马秋千,绳索AB的长为5米.若将它沿水平方向向前推进3米(即DE=3米),且绳索保持拉直的状态,则此时木马上升的高度为(
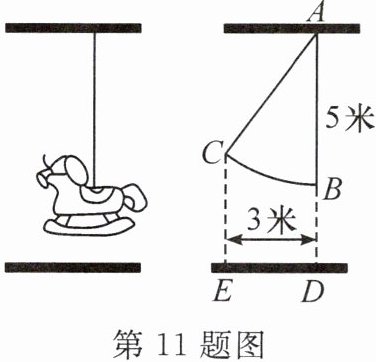
A.1米
B.1.5米
C.2米
D.4米
A
)
A.1米
B.1.5米
C.2米
D.4米
答案:
A
12. (2024·贵阳乌当区期中)对角线互相垂直的四边形叫作“垂美”四边形,现有如图所示的“垂美”四边形ABCD,对角线AC,BD交于点O.若AD=2,BC=4,则AB²+CD²=
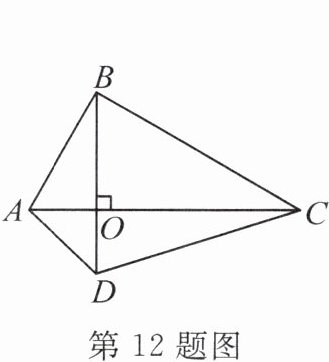
20
.
答案:
20
13. (教材P21新增复习题T8变式)《九章算术》卷九“勾股”中记载:“今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐,问水深、葭长各几何?”大意:如图,水池底面的宽AB=1丈,芦苇OC生长在AB的中点O处,高出水面的部分CD=1尺.将芦苇向池岸牵引,尖端达到岸边时恰好与水面平齐,即OC=OE,求水池的深度和芦苇的长度.(1丈=10尺).
(1)求水池的深度OD.
(2)我国古代数学家刘徽在为《九章算术》作注解时,更进一步给出了这类问题的一般解法.他的解法用现代符号语言可以表示为:若已知水池宽AB=2a,芦苇高出水面的部分CD=n(n<a),则水池的深度OD(OD=b)可以通过公式b=$\frac{a^{2}-n^{2}}{2n}$计算得到.请说明刘徽解法的正确性.
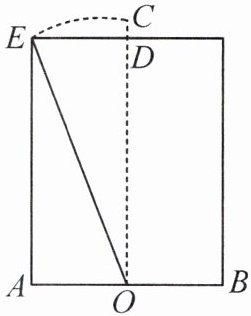
(1)求水池的深度OD.
(2)我国古代数学家刘徽在为《九章算术》作注解时,更进一步给出了这类问题的一般解法.他的解法用现代符号语言可以表示为:若已知水池宽AB=2a,芦苇高出水面的部分CD=n(n<a),则水池的深度OD(OD=b)可以通过公式b=$\frac{a^{2}-n^{2}}{2n}$计算得到.请说明刘徽解法的正确性.

答案:
解:
(1)设芦苇的长为$x$尺,则$OC = OE = x$尺,$OD=(x - 1)$尺,$DE = 5$尺。在$Rt\triangle ODE$中,$\angle ODE = 90^{\circ}$,由勾股定理,得$DE^{2}+OD^{2}=OE^{2}$,$\therefore5^{2}+(x - 1)^{2}=x^{2}$,解得$x = 13$。$\therefore OD = 13 - 1 = 12$(尺)。答:水池的深度$OD$为$12$尺。
(2)$\because OD = b$,$CD = n$,$AB = 2a$,$\therefore OC = OE = b + n$,$DE = a$。在$Rt\triangle ODE$中,$\angle ODE = 90^{\circ}$,由勾股定理,得$DE^{2}+OD^{2}=OE^{2}$,$\therefore a^{2}+b^{2}=(b + n)^{2}$,解得$b=\frac{a^{2}-n^{2}}{2n}$。
(1)设芦苇的长为$x$尺,则$OC = OE = x$尺,$OD=(x - 1)$尺,$DE = 5$尺。在$Rt\triangle ODE$中,$\angle ODE = 90^{\circ}$,由勾股定理,得$DE^{2}+OD^{2}=OE^{2}$,$\therefore5^{2}+(x - 1)^{2}=x^{2}$,解得$x = 13$。$\therefore OD = 13 - 1 = 12$(尺)。答:水池的深度$OD$为$12$尺。
(2)$\because OD = b$,$CD = n$,$AB = 2a$,$\therefore OC = OE = b + n$,$DE = a$。在$Rt\triangle ODE$中,$\angle ODE = 90^{\circ}$,由勾股定理,得$DE^{2}+OD^{2}=OE^{2}$,$\therefore a^{2}+b^{2}=(b + n)^{2}$,解得$b=\frac{a^{2}-n^{2}}{2n}$。
14. 新考向 数学文化(2024·贵阳乌当区期末)图1是东汉末年数学家刘徽根据“割补术”,运用数形关系证明勾股定理时的青朱出入图,图中的两个青入的三角形分别与两个青出的三角形全等,朱入与朱出的三角形全等,朱方与青方是两个正方形,探究学习时,标上字母绘成图2.若记朱方对应正方形GDJH的边长为a,青方对应正方形ABCD的边长为b,已知b-a=3,a²+b²=29,则图2中阴影部分的面积为
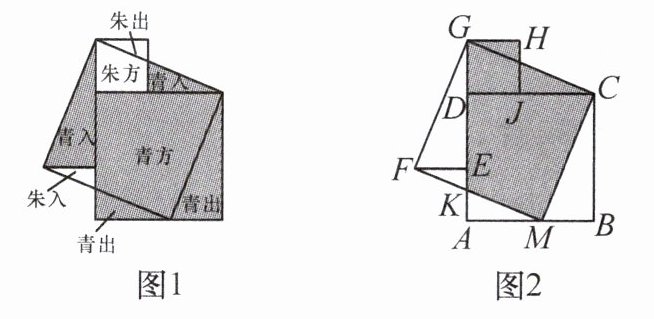
24
.
答案:
24
查看更多完整答案,请扫码查看


