《2025年名校课堂八年级数学上册北师大版贵州专版》

9. (教材P28新增随堂练习T2变式)在实数0，1，$-\pi$，-2中，最小的数是(C)

A.0
B.1
C.$-\pi$
D.-2

答案： C

10. 下列说法正确的是(B)

A.实数$-a$是负数
B.实数$-a$的相反数是$a$
C.实数$-a$的绝对值是$a$
D.$|-a|$一定是正数

答案： B

11. 已知无理数$a = 1.414213562\cdots$，$b = 3.31662479\cdots$，则$b - a\approx$1.90。(结果保留小数点后两位)

答案： 1.90

12. 若数$a$可以在数轴上表示出来，则$a$一定为(D)

A.有理数
B.无理数
C.分数
D.实数

答案： D

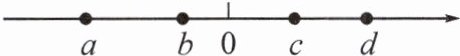
13. (2024·深圳)如图，实数$a$，$b$，$c$，$d$在数轴上表示如下，则其中最小的实数为(A)


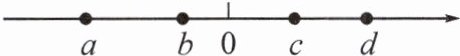
A.$a$
B.$b$
C.$c$
D.$d$

答案： A

14. 下列各数中，是无理数的是(D)

A.体积为8的正方体的棱长
B.面积为36的正方形的边长
C.长、宽分别为12，5的长方形对角线的长
D.半径为3的圆的周长

答案： D

15. 判断下列说法是否正确。若正确，请说明理由；若不正确，请举例说明。
（1）两个整数相除，如果永远都除不尽，那么结果一定是一个无理数。
（2）任意一个无理数的绝对值都是正数。

答案： （1）不正确.例如：$\frac{1}{3}=0.\overset{.}{3}$，但$\frac{1}{3}$是有理数.（2）正确.因为任意一个非零实数的绝对值为正数，无理数均为非零实数.

16. 已知$|x| ＜ \pi$（$x$是整数），求$x$的值，并在数轴上表示求得的数。

答案：
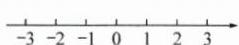
$\because|x|\lt\pi,\pi\approx3.14$，且$x$是整数，$\therefore x=-3,-2,-1,0,1,2,3$.将求得的数表示在数轴上如图：

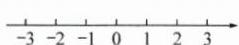
17. 已知某个长方体的体积是$1800\mathrm{cm}^3$，它的长、宽、高之比是$5:4:3$，则该长方体的长、宽、高是有理数还是无理数？为什么？

答案： 该长方体的长、宽、高都是无理数.理由如下：设长方体的长、宽、高分别为$5x\ cm,4x\ cm,3x\ cm$.根据题意，得$5x\cdot4x\cdot3x = 1800$，则$x^{3}=30$.$\because$不存在一个有理数的立方为$30$，$\therefore x$是无理数.$\therefore5x,4x,3x$均为无理数，即该长方体的长、宽、高都是无理数.

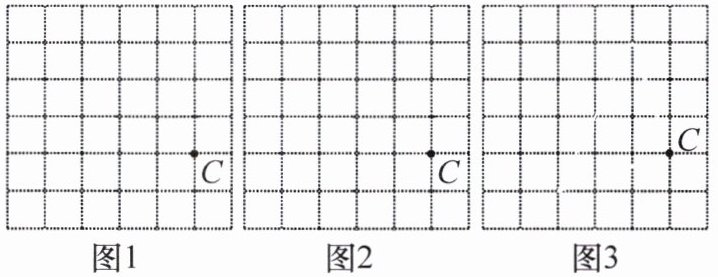
18. 如图，在正方形网格中，每个小正方形的边长均为1。已知点C，请按要求设计$\triangle ABC，$使$\angle ACB = 90°，$AC = BC。
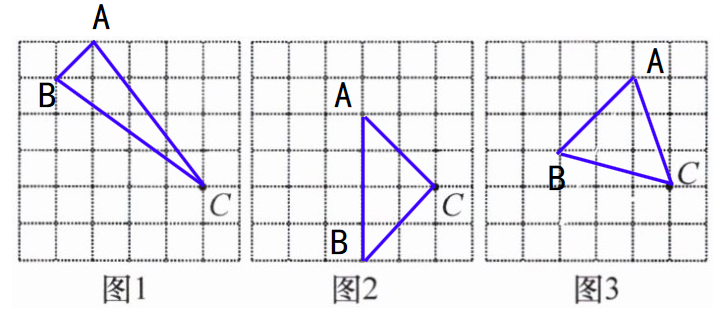
（1）在图1中，AB的长为无理数，AC，BC的长均为有理数。
（2）在图2中，AB的长为有理数，AC，BC的长均为无理数。
（3）在图3中，三边的长均为无理数。

答案：