《2025年名校课堂八年级数学上册北师大版贵州专版》

12. 计算：$\sqrt{1\frac{9}{16}}=$$\frac{5}{4}$.

答案： $\frac{5}{4}$

13. 若$\sqrt{a^{2}}=5$，则$a$的值为 (B)

A.5
B.±5
C.±$\sqrt{5}$
D.-5

答案： B

14. 若一个正方形的面积扩大为原来的 3 倍，则它的边长要扩大为原来的倍 (B)

A.3
B.$\sqrt{3}$
C.2
D.9

答案： B

15. 如图，这是一个数值转换器，当输入$x$的值为 9 时，输出$y$的值是 (C)


A.3
B.-$\sqrt{3}$
C.$\sqrt{3}$
D.-3

答案： C

16. 若一个数的算术平方根是它本身，则这个数是0或1.

答案： 0或$1$

17. 若$|a|=5$，$\sqrt{b}=3$，$ab＜0$，则$a+b=$4.

答案： 4

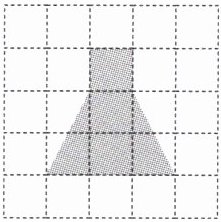
18. 如图，每个小正方形的边长为 1，把阴影部分剪下来，再用剪下来的阴影部分继续剪拼成一个正方形，那么新正方形的边长是$\sqrt{5}$.

答案： $\sqrt{5}$

19. 如图，Rt$\triangle ABC$中，$∠B=90^{\circ}$，$AB=5\ cm$，$BC=6\ cm$，点$P$从点$B$出发，沿$BA$以$1\ cm/s$的速度向点$A$运动，同时点$Q$从点$B$出发，沿$BC$以$2\ cm/s$的速度向点$C$运动. 几秒后，$\triangle PBQ$的面积为$9\ cm^{2}$？

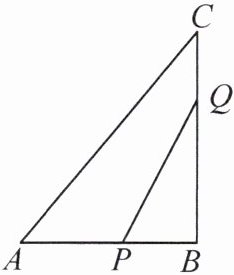
答案： 设$t$s后，$\triangle PBQ$的面积为$9cm^{2}$，此时$BP = tcm$，$BQ = 2tcm$。根据题意，得$\frac{1}{2}\cdot t\cdot2t = 9$。整理，得$t^{2}=9$，
∴$t=\sqrt{9}=3$。当$t = 3$时，$t = 3＜5$，$2t = 2×3 = 6$，符合题意。答：$3$s后，$\triangle PBQ$的面积为$9cm^{2}$。

20. 我们知道，负数没有算术平方根，但对于三个互不相等的负整数，若两两乘积的算术平方根都是整数，则称这三个数为“完美组合数”. 例如：-9，-4，-1 这三个数，$\sqrt{(-9)×(-4)}=6$，$\sqrt{(-9)×(-1)}=3$，$\sqrt{(-4)×(-1)}=2$，其结果 6，3，2 都是整数，所以 -9，-4，-1 这三个数是“完美组合数”.
(1)-25，-4，-1 这三个数是“完美组合数”吗？请说明理由.
(2)若-80，$a$，-5 是“完美组合数”，其中有两个数乘积的算术平方根为 10，求$a$的值.

答案：
(1)是“完美组合数”。理由如下：
∵$\sqrt{(-25)×(-4)} = 10$，$\sqrt{(-25)×(-1)} = 5$，$\sqrt{(-4)×(-1)} = 2$，且$10$，$5$，$2$都是整数，
∴$-25$，$-4$，$-1$这三个数是“完美组合数”。
(2)分两种情况讨论：①当$\sqrt{(-80)\cdot a}=10$时，$-80a = 100$，解得$a = -\frac{5}{4}$，不符合题意，舍去；②当$\sqrt{(-5)\cdot a}=10$时，$-5a = 100$，解得$a = -20$。此时$\sqrt{(-20)×(-80)} = 40$，$\sqrt{(-5)×(-80)} = 20$，且$10$，$40$，$20$都是整数，
∴$-80$，$-20$，$-5$是“完美组合数”，符合题意。综上所述，$a$的值为$-20$。