《2025年同步练习册山东教育出版社七年级数学上册人教版》

3. 某书店新进了一批图书，甲、乙两种书的进价分别为 $4$ 元/本、$10$ 元/本。现购进 $m$ 本甲种书和 $n$ 本乙种书，共付款 $P$ 元。
(1)用含 $m$，$n$ 的代数式表示 $P$，则 $P=$$4m+10n$元；
(2)若共购进 $5×10^{2}$ 本甲种书及 $3×10^{2}$ 本乙种书，用科学记数法表示 $P$ 的值，则 $P=$$5×10^{3}$元。

答案： （1）$4m+10n$ （2）$5×10^{3}$

4. 某村经济作物合作社大豆种植面积是 $a$ 公顷，水稻种植面积是大豆种植面积的 $2$ 倍，玉米种植面积比大豆种植面积少 $5$ 公顷。
(1)水稻种植面积为$2a$公顷，玉米种植面积为$a-5$公顷；
(2)若 $a = 10$ 公顷，求三种经济作物的种植总面积。

答案： （1）$2a$ $a-5$ （2）35公顷

5. 为节约能源，某市按如下规定收取电费：如果每月用电不超过 $140$ 千瓦时，按每千瓦时 $0.53$ 元收费；如果超过 $140$ 千瓦时，则超过部分按每千瓦时 $0.67$ 元收费。
（1）若某住户 $4$ 月的用电量为 $a$ 千瓦时，已知 $a$ 小于 $140$ 千瓦时，求该住户 $4$ 月应缴的电费；
（2）若该住户 $5$ 月的用电量是 $200$ 千瓦时，则 $5$ 月应缴电费多少元？

答案： （1）该住户4月应缴电费$0.53a$。
（2）当$a=200$时，应缴电费$140×0.53+0.67(200-140)=114.4$（元）。

6. 铜钱是我国的早期货币，外圆内方的构造彰显了数学之美，如示意图。铜钱外部的圆半径为 $a$，里边正方形的边长为 $b$。
（1）请用含有 $a$，$b$ 的式子表示图中阴影部分的面积；
（2）当 $a = 3$，$b = 1$，则图中阴影部分的面积是多少？（$\pi\approx3$）

答案： （1）由题意可得，图中阴影部分的面积为$\pi a^{2}-b^{2}$。
（2）当$a=3$，$b=1$时，原式$=3×3^{2}-1^{2}=26$。因此，图中阴影部分的面积是26。

7. 国庆期间，广场上设置了一个庆祝国庆的造型(如图所示)。造型平面成轴对称，它的正中间为一个半径为 $b$ 的半圆，摆放花草，其余部分为展板。求：
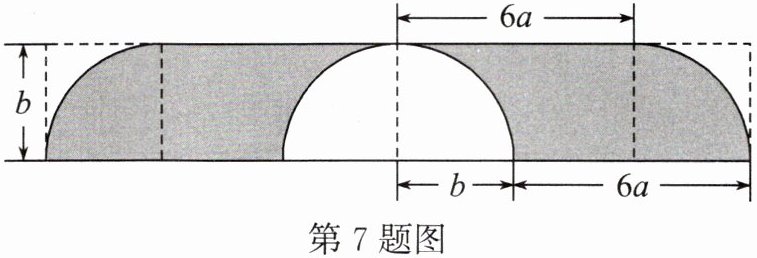
(1)展板的面积是$12ab$；(用含 $a$，$b$ 的代数式表示)
(2)若 $a = 0.5$ 米，$b = 2$ 米，求展板的面积；
(3)在(2)的条件下，已知摆放花草部分造价为 $450$ 元/平方米，展板部分造价为 $80$ 元/平方米，求制作整个造型的造价。($\pi$ 取 $3$)

答案： （1）$12ab$
（2）当$a=0.5$米，$b=2$米时，展板的面积$=12×0.5×2=12$（平方米）。
（3）制作整个造型的造价为$12×80+\frac{1}{2}\pi×4×450=3660$（元）。