第54页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
9. 观察下列等式:
$ 3^{1} = 3 $,$ 3^{2} = 9 $,$ 3^{3} = 27 $,$ 3^{4} = 81 $,$ 3^{5} = 243 $,$ 3^{6} = 729 $,$ 3^{7} = 2187 $。
解答下列问题:$ 3^{1} + 3^{2} + 3^{3} + 3^{4} + \cdots + 3^{2024} $ 的个位数字是(
A.$ 0 $
B.$ 1 $
C.$ 3 $
D.$ 7 $
$ 3^{1} = 3 $,$ 3^{2} = 9 $,$ 3^{3} = 27 $,$ 3^{4} = 81 $,$ 3^{5} = 243 $,$ 3^{6} = 729 $,$ 3^{7} = 2187 $。
解答下列问题:$ 3^{1} + 3^{2} + 3^{3} + 3^{4} + \cdots + 3^{2024} $ 的个位数字是(
A
)。A.$ 0 $
B.$ 1 $
C.$ 3 $
D.$ 7 $
答案:
A
10. 观察下列式子:
$ 1 × 3 + 1 = 2^{2} $;
$ 7 × 9 + 1 = 8^{2} $;
$ 25 × 27 + 1 = 26^{2} $;
$ 79 × 81 + 1 = 80^{2} $;
$ \cdots \cdots $
可猜想第 $ 2024 $ 个式子为
$ 1 × 3 + 1 = 2^{2} $;
$ 7 × 9 + 1 = 8^{2} $;
$ 25 × 27 + 1 = 26^{2} $;
$ 79 × 81 + 1 = 80^{2} $;
$ \cdots \cdots $
可猜想第 $ 2024 $ 个式子为
$(3^{2024}-2)×3^{2024}+1=(3^{2024}-1)^2$
。
答案:
$(3^{2024}-2)×3^{2024}+1=(3^{2024}-1)^2$
11. 将全体正奇数排成一个三角形数阵:
$\begin{array}{ccccccc}& & & 1 & & & \\& & 3 & & 5 & & \\& 7 & & 9 & & 11 & \\13 & & 15 & & 17 & & 19 \\& & & \cdots & & &\end{array}$
按照以上排列的规律,第 $ 25 $ 行第 $ 20 $ 个数是
$\begin{array}{ccccccc}& & & 1 & & & \\& & 3 & & 5 & & \\& 7 & & 9 & & 11 & \\13 & & 15 & & 17 & & 19 \\& & & \cdots & & &\end{array}$
按照以上排列的规律,第 $ 25 $ 行第 $ 20 $ 个数是
639
。
答案:
639
12. (1)规定:求若干个相同的有理数(均不等于 $ 0 $)的除法运算叫做除方,如 $ 2 ÷ 2 ÷ 2 $,$ (-3) ÷ (-3) ÷ (-3) ÷ (-3) $ 等。类比有理数的乘方,我们把 $ 2 ÷ 2 ÷ 2 $ 记作 $ 2^{\circledcirc 3} $,读作“$ 2 $ 的圈 $ 3 $ 次方”;$ (-3) ÷ (-3) ÷ (-3) ÷ (-3) $ 记作 $ (-3)^{\circledcirc 4} $,读作“$ -3 $ 的圈 $ 4 $ 次方”。一般地,把 $ \underbrace{a ÷ a ÷ a ÷ \cdots ÷ a}_{n 个 a} (a \neq 0) $ 记作 $ a^{\circledcirc n} $,读作“$ a $ 的圈 $ n $ 次方”。
① 直接写出计算结果:
$ 2^{\circledcirc 3} = $
② 关于除方,下列说法错误的是(
A. 任何非零数的圈 $ 3 $ 次方都等于它的倒数
B. 对于任何正整数 $ n $,$ 1^{\circledcirc n} = 1 $
C. $ 3^{\circledcirc 4} > 4^{\circledcirc 3} $
D. 负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数
(2)我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?
$\begin{array}{c}\boxed{除方} \\2^{\circledcirc 4} = 2 ÷ 2 ÷ 2 ÷ 2 \\= 2 × \dfrac{1}{2} × \dfrac{1}{2} × \dfrac{1}{2} \\= \left( \dfrac{1}{2} \right)^{2} \\\boxed{乘方幂的形式}\end{array}$
① 试一试:仿照上面的算式,将下列运算结果直接写成幂的形式。
$ (-3)^{\circledcirc 4} = $
② 想一想:将一个非零有理数 $ a $ 的圈 $ n (n \geq 3) $ 次方写成幂的形式等于
③ 算一算:$ 12^{2} ÷ \left( -\dfrac{1}{3} \right)^{\circledcirc 4} × \left( -\dfrac{1}{2} \right)^{\circledcirc 5} + \left( -\dfrac{1}{3} \right)^{\circledcirc 6} ÷ 3^{3} $。
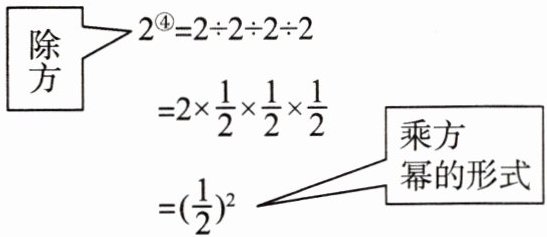
① 直接写出计算结果:
$ 2^{\circledcirc 3} = $
$\dfrac{1}{2}$
;$ \left( -\dfrac{1}{2} \right)^{\circledcirc 5} = $$-8$
。② 关于除方,下列说法错误的是(
C
)。A. 任何非零数的圈 $ 3 $ 次方都等于它的倒数
B. 对于任何正整数 $ n $,$ 1^{\circledcirc n} = 1 $
C. $ 3^{\circledcirc 4} > 4^{\circledcirc 3} $
D. 负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数
(2)我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?
$\begin{array}{c}\boxed{除方} \\2^{\circledcirc 4} = 2 ÷ 2 ÷ 2 ÷ 2 \\= 2 × \dfrac{1}{2} × \dfrac{1}{2} × \dfrac{1}{2} \\= \left( \dfrac{1}{2} \right)^{2} \\\boxed{乘方幂的形式}\end{array}$
① 试一试:仿照上面的算式,将下列运算结果直接写成幂的形式。
$ (-3)^{\circledcirc 4} = $
$\left(-\dfrac{1}{3}\right)^2$
;$ 5^{\circledcirc 6} = $$\left(\dfrac{1}{5}\right)^4$
;$ \left( -\dfrac{1}{2} \right)^{\circledcirc 10} = $$(-2)^8$
。② 想一想:将一个非零有理数 $ a $ 的圈 $ n (n \geq 3) $ 次方写成幂的形式等于
$\left(\dfrac{1}{a}\right)^{n-2}$
。③ 算一算:$ 12^{2} ÷ \left( -\dfrac{1}{3} \right)^{\circledcirc 4} × \left( -\dfrac{1}{2} \right)^{\circledcirc 5} + \left( -\dfrac{1}{3} \right)^{\circledcirc 6} ÷ 3^{3} $。
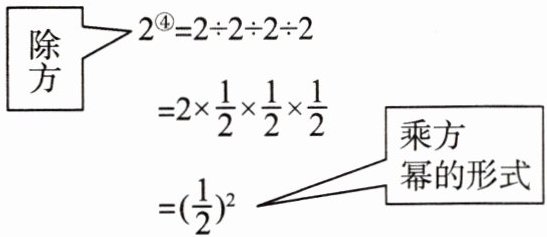
答案:
(1)①$\dfrac{1}{2}$;$-8$;②C;(2)①$\left(-\dfrac{1}{3}\right)^2$;$\left(\dfrac{1}{5}\right)^4$;$(-2)^8$;②$\left(\dfrac{1}{a}\right)^{n-2}$;③解:原式$=12×12÷(-3)^2×(-2)^3+(-3)^4÷3^3=-144÷9×8+81÷27=-128+3=-125$
查看更多完整答案,请扫码查看


