第71页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
17. (8分)如图,平面上有四个点A,B,C,D,根据下列语句画图:
(1)画直线AB;
(2)画射线AC;
(3)连接BC并延长BC到E,使得$ CE = AB + BC $;
(4)在线段BD上取点P,使$ PA + PC $的值最小.
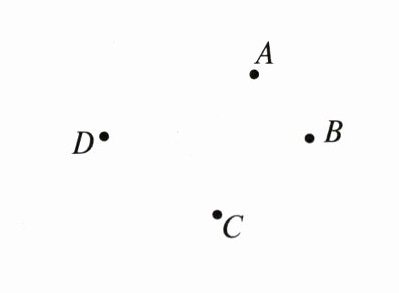
(1)画直线AB;
(2)画射线AC;
(3)连接BC并延长BC到E,使得$ CE = AB + BC $;
(4)在线段BD上取点P,使$ PA + PC $的值最小.

答案:
17.解
(1)至
(4)题,如图所示.

17.解
(1)至
(4)题,如图所示.

18. (6分)如图,O是直线AB上一点,OD平分$ \angle BOC $,$ \angle COE = 90^{\circ} $.若$ \angle AOC = 30^{\circ} $.
(1)求$ \angle DOE $的度数;
(2)图中互为余角的角有
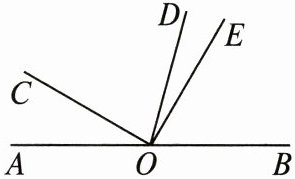
(1)求$ \angle DOE $的度数;
(2)图中互为余角的角有
3
对.
答案:
18.解
(1)因为∠AOC=30°,
所以∠BOC=180° - ∠AOC=150°.
因为OD平分∠BOC,所以∠COD=$\frac{1}{2}$∠BOC=75°.
因为∠COE=90°,所以∠DOE=90° - 75°=15°.
(2)因为∠COE=90°,所以∠AOC+∠BOE=90°,∠COD+∠DOE=90°.
因为OD平分∠BOC,所以∠COD=∠BOD,
所以∠BOD+∠DOE=90°,
所以图中互为余角的角有∠AOC和∠BOE,∠COD和∠DOE,∠BOD和∠DOE,共3对.
故答案为3.
(1)因为∠AOC=30°,
所以∠BOC=180° - ∠AOC=150°.
因为OD平分∠BOC,所以∠COD=$\frac{1}{2}$∠BOC=75°.
因为∠COE=90°,所以∠DOE=90° - 75°=15°.
(2)因为∠COE=90°,所以∠AOC+∠BOE=90°,∠COD+∠DOE=90°.
因为OD平分∠BOC,所以∠COD=∠BOD,
所以∠BOD+∠DOE=90°,
所以图中互为余角的角有∠AOC和∠BOE,∠COD和∠DOE,∠BOD和∠DOE,共3对.
故答案为3.
19. (8分)如图,C为线段AB延长线上一点,D为线段BC上一点,$ AB = 12 $,$ CD = 4BD $.
(1)若$ BC = 15 $,求AD的长;
(2)若$ AB = 2BD $,E为线段AC的中点,求BE的长.
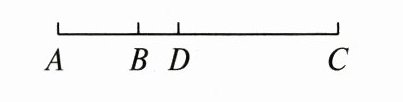
(1)若$ BC = 15 $,求AD的长;
(2)若$ AB = 2BD $,E为线段AC的中点,求BE的长.
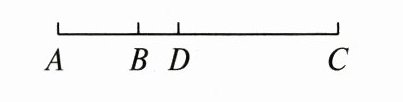
答案:
19.解
(1)因为CD=4BD,
所以BC=BD+CD=5BD.
因为BC=15,所以BD=3.
因为AB=12,所以AD=AB+BD=15.
(2)因为AB=2BD=12,所以BD=6.
所以CD=4BD=24,所以AC=AB+BD+CD=42.
因为E是线段AC的中点,
所以AE=$\frac{1}{2}$AC=21,所以BE=AE - AB=9.
(1)因为CD=4BD,
所以BC=BD+CD=5BD.
因为BC=15,所以BD=3.
因为AB=12,所以AD=AB+BD=15.
(2)因为AB=2BD=12,所以BD=6.
所以CD=4BD=24,所以AC=AB+BD+CD=42.
因为E是线段AC的中点,
所以AE=$\frac{1}{2}$AC=21,所以BE=AE - AB=9.
20. (8分)由棱长都为1 cm的9个小正方体组成的简单几何体,如图所示.
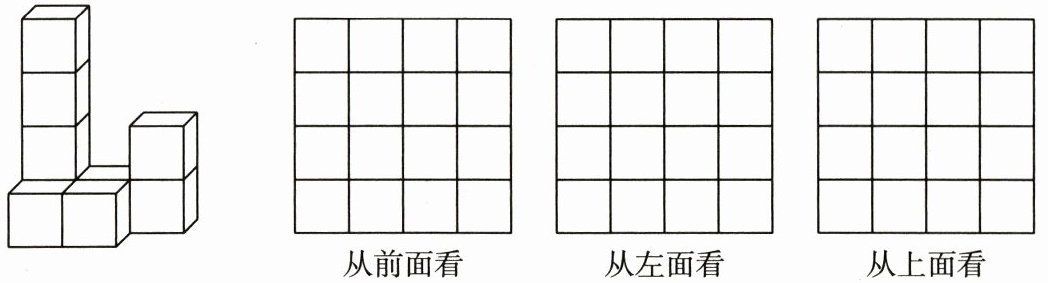
(1)求这个几何体的表面积;
(2)按要求在方格中画出这个几何体从不同的方向看到的平面图形.

(1)求这个几何体的表面积;
(2)按要求在方格中画出这个几何体从不同的方向看到的平面图形.
答案:
20.解
(1)这个组合体的表面积为(7+5+5)×2+2=36($cm^2$).
(2)从不同方向看这个几何体所得到的平面图形如下.



20.解
(1)这个组合体的表面积为(7+5+5)×2+2=36($cm^2$).
(2)从不同方向看这个几何体所得到的平面图形如下.



查看更多完整答案,请扫码查看


