《2025年学习目标与检测同步测试卷七年级数学上册人教版》

21. (10分)一次数学课外活动中,小红所在的小组到眼镜店调查了一些数据,整理成下面的统计表:

(1)镜片焦距是怎样随着眼镜度数的变化而变化的?
(2)用式子表示$y$与$x$的关系,$y$与$x$成什么比例关系?
(3)若小红的眼镜度数为1000度,求该副眼镜的镜片焦距.

答案： 21.解
(1)镜片焦距随着眼镜度数的增大而减小。
(2)$xy = 100$，$y$与$x$成反比例关系。
(3)令$y = 1000$，则$1000x = 100$，解得$x = 0.1$，故该副眼镜的镜片焦距是0.1mm。

22. (10分)近年来,电商多选择在11月11日促销.今年促销期间,某电商仓库打包员在为买家包装商品时用到长、宽、高分别为$a$cm,$b$cm,$c$cm的箱子,并发现有图中所示的甲、乙两种打包方式(打包带接头处的长度忽略不计).回答下列问题:
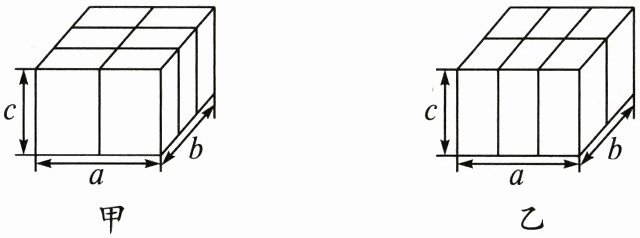
(1)用含$a$,$b$,$c$的式子分别表示甲、乙两种打包方式所用的打包带的长度;
(2)当$a = 50$,$b = 40$,$c = 30$时,计算出甲、乙两种打包方式所用的打包带的长度;
(3)当$a＞b＞c$时,两种打包方式中,哪种打包方式节省打包带? 并说明你的理由.

答案： 22.解
(1)甲种打包方式所用的打包带长度为$(4a + 2b + 6c)$cm，乙种打包方式所用的打包带长度为$(2a + 4b + 6c)$cm。
(2)当$a = 50,b = 40,c = 30$时，$4a + 2b + 6c = 4×50 + 2×40 + 6×30 = 460$。
当$a = 50,b = 40,c = 30$时，$2a + 4b + 6c = 2×50 + 4×40 + 6×30 = 440$。
故甲、乙两种打包方式所用的打包带的长度分别是
460cm和440cm。
(3)乙种打包方式节省打包带，理由如下：
因为$4a + 2b + 6c$与$2a + 4b + 6c$中都有$6c$，所以只比较
$4a + 2b$与$2a + 4b$即可。
因为$a＞b$，所以$4a + 2b＞2a + 4b$，所以乙种打包方式节
省打包带。