《2025年学习目标与检测同步测试卷七年级数学上册人教版》

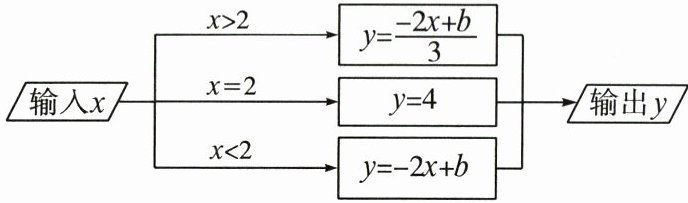
9. 根据图中所示的程序计算,若输入的$x$值为$-1$时,输出的值为$3$,则输入的值为$5$时,输出的值为(C)


A.$-1$
B.$1$
C.$-3$
D.$4$

答案： 9.C 解析 因为输入的$x$值为$-1$时，输出的值为$3$，所以$-2 × (-1) + b = 3$，所以$b = 1$. 当输入的值为$5$时，输出的值为$\frac{-2 × 5 + 1}{3} = -3$. 故选C.

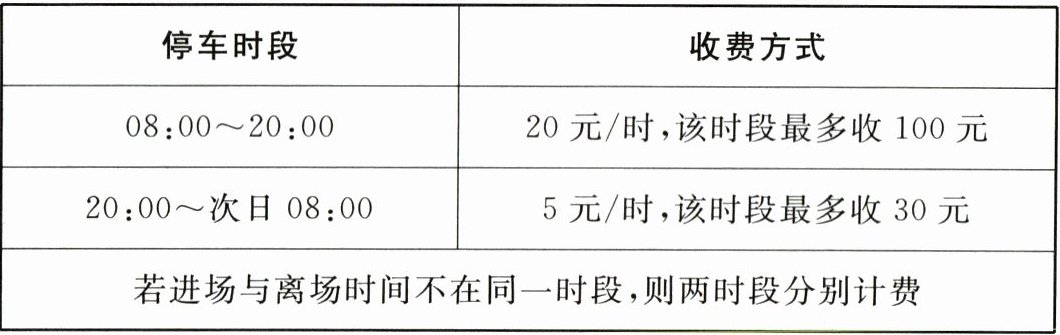
10. 某停车场$24$小时营业,其收费方式如表所示,已知李女士某日$10:00$进场停车,停了$x$小时后离场,$x$为整数.若李女士离场时间介于当日的$20:00\sim24:00$间,则她此次停车的费用为(B)


A.$[200 + 5(x - 10)]$元
B.$[100 + 5(x - 10)]$元
C.$[100 + 5(x - 20)]$元
D.$[200 + 5(x - 20)]$元

答案： 10.B 解析 由题意得李女士停车的时间超过$5$小时，且第二个时段的停车时间为$(x - 10)$小时. 因为李女士离场时间介于当日的$20:00 \sim 24:00$间，所以李女士的停车费为$[100 + 5(x - 10)]$元. 故选B.

11. 下列式子是代数式的是①②⑤.(填序号)
①$a^{2}+b^{2}$ ②$\frac{s}{t}$ ③$x - 1\lt0$ ④$x = 2$ ⑤$13$

答案： 11.①②⑤

12. 已知等边三角形的边长为$p$,正方形的边长为$q$,则$3p + 4q$的实际意义为等边三角形的周长与正方形的周长之和.

答案： 12.等边三角形的周长与正方形的周长之和

13. 甲、乙两地相距$n\ km$,提速前火车从甲地到乙地要用$t\ h(t\gt1)$,提速后两地间的行车时间减少了$1\ h$,则提速后火车的速度比提速前的快了$\frac{n}{t - 1} - \frac{n}{t}$$km/h$.

答案： 13.$\frac{n}{t - 1} - \frac{n}{t}$ 解析 提速前的速度为$\frac{n}{t} km/h$，提速后的速度为$\frac{n}{t - 1} km/h$，
提速后火车的速度比提速前的快了$(\frac{n}{t - 1} - \frac{n}{t}) km/h$.

14. 若$x^{2}-2x - 2 = 0$,则代数式$x^{2}-2x + 2025$的值是2027.

答案： 14.$2027$ 解析 因为$x^2 - 2x - 2 = 0$，所以$x^2 - 2x = 2$.
所以$x^2 - 2x + 2025 = 2 + 2025 = 2027$.

15. 如果$x=\frac{1}{3}y$,那么$x$和$y$成正比例关系;如果$\frac{1}{y}=\frac{x}{3}$,那么$x$和$y$成反比例关系.

答案： 15.正 反 解析 如果$x = \frac{1}{3}y$，则$\frac{y}{x} = 3$，比值一定，故$x$和$y$成正比例关系；如果$\frac{1}{y} = \frac{x}{3}$，则$xy = 3$，乘积一定，故$x$和$y$成反比例关系.

16. 某种杆秤的示意图如图所示.在秤杆的点$A$处固定提纽,点$B$处挂秤盘,点$C$为$0$刻度点.当秤盘不放物品时,提起提纽,秤砣所挂位置移动到点$C$,秤杆处于平衡.秤盘放入$x$克物品后移动秤砣,当秤砣所挂位置与提纽的距离为$y$毫米时秤杆处于平衡.测得$x$与$y$的几组对应数据如下表:


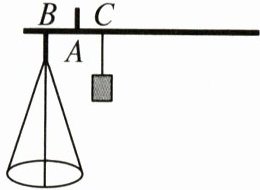
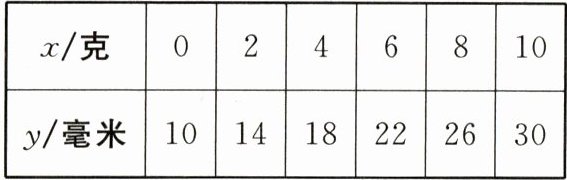
由表中数据的规律可知,当$x = 20$克时,$y=$50毫米.

答案： 16.$50$ 解析 由题可得当放入$0$克物品时，秤砣所挂位置与提纽的距离为$10$毫米，当放入$2$克物品时，秤砣所挂位置与提纽的距离为$10 + 2 × 2 = 14$（毫米），当放入$4$克物品时，秤砣所挂位置与提纽的距离为$10 + 2 × 4 = 18$（毫米），当放入$6$克物品时，秤砣所挂位置与提纽的距离为$10 + 2 × 6 = 22$（毫米），当放入$8$克物品时，秤砣所挂位置与提纽的距离为$10 + 2 × 8 = 26$（毫米），当放入$10$克物品时，秤砣所挂位置与提纽的距离为$10 + 2 × 10 = 30$（毫米）……
所以当放入$x$克物品时，秤砣所挂位置与提纽的距离为$(10 + 2x)$毫米，当$x = 20$时，秤砣所挂位置与提纽的距离为$10 + 2 × 20 = 50$（毫米）.