《2025年学习目标与检测同步测试卷七年级数学上册人教版》

21. (8分)某校七年级1至4班计划每班购买数量相同的图书布置班级读书角,但是由于种种原因,实际购书量与计划有出入,实际购书情况如表所示:

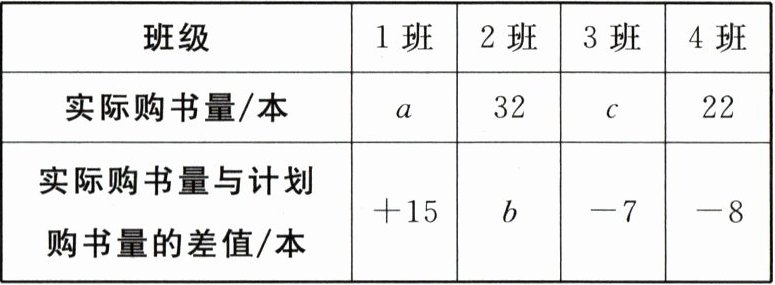
(1) $a=$45,$b=$+2,$c=$23;
(2) 根据记录的数据可知4个班实际购书共122本;
(3) 书店给出一种优惠方案:一次购买达到15本,其中2本书免费.若每本书售价为30元,求这4个班团体购书的最低费用.

答案： 21.解
(1)每个班计划购书量为$22-(-8)=22+8=30$(本)，故$a=30+15=45$，$b=32-30=+2$，$c=30-7=23$。故答案为45，+2，23。
(2)4个班实际购书共$45+32+23+22=122$(本)。故答案为122。
(3)如果每次购买15本，那么可以购买8次，且最后还剩2本书单独购买，即这4个班团体购书的最低费用为$30 × (15-2) × 8+30 × 2=3120+60=3180$(元)。

22. (10分)阅读下面的材料.
在学习绝对值时,根据绝对值的几何意义,我们知道$|5-3|$表示5与3在数轴上对应的两点之间的距离;$|5+3|=|5-(-3)|$,所以$|5+3|$表示5与-3在数轴上对应的两点之间的距离;$|5|=|5-0|$,所以$|5|$表示5在数轴上对应的点到原点的距离.一般地,点A,B在数轴上分别表示有理数a,b,那么A,B两点之间的距离可以表示为$|a-b|$.
回答下列问题:
(1) 数轴上表示6与-9的两点之间的距离是15;数轴上表示$x$与2的两点之间的距离是|x-2|.
(2) 若$|x-3|=3$,则$x=$6或0.
(3) 满足$|x+2|+|x-3|=5$的有理数$x$有多少个?

答案： 22.解
(1)数轴上表示6与$-9$的两点之间的距离是$|6-(-9)|=|6+9|=|15|=15$，数轴上表示$x$与2的两点之间的距离是$|x-2|$。故答案为15，$|x-2|$。
(2)因为$|x-3|=3$，所以$x$与3在数轴上对应的两点之间的距离为3，所以$x=6$或$x=0$。故答案为6或0。
(3)因为$|x+2|+|x-3|=5$，所以数轴上表示$x$与$-2$的两点之间的距离与数轴上表示$x$与3的两点之间的距离和为5，所以$x$在$-2$与3之间(包括$-2$和3两个数)，所以这样的有理数$x$有无数个。