《2025年学习目标与检测同步测试卷七年级数学上册人教版》

7. 将$-2-(+5)-(-7)+(-9)$写成省略括号的形式是(D)

A.$-2+5-7-9$
B.$-2-5+7+9$
C.$-2-5-7-9$
D.$-2-5+7-9$

答案： 7.D 解析$- 2 - ( + 5 ) - ( - 7 ) + ( - 9 ) = - 2 - 5 + 7 - 9$．故选D．

8. 计算$(-5)÷(-5)×(-\frac{1}{5})$的结果为(B)

A.$-1$
B.$-\frac{1}{5}$
C.$-125$
D.$-\frac{1}{125}$

答案： 8.B 解析$( - 5 ) ÷ ( - 5 ) × ( - \frac { 1 } { 5 } ) = 1 × ( - \frac { 1 } { 5 } ) = - \frac { 1 } { 5 }$．故选B．

9. 要使算式$(-1)□3$的运算结果最大,则$□$内应填入的运算符号为(A)

A.$+$
B.$-$
C.$×$
D.$÷$

答案： 9.A 解析当填“$+$”时，$( - 1 ) + 3 = 2$；当填“$-$”时，$( - 1 ) - 3 = - 4$；当填“$×$”时，$( - 1 ) × 3 = - 3$；当填“$÷$”时，$( - 1 ) ÷ 3 = - \frac { 1 } { 3 }$．因为$2 ＞ - \frac { 1 } { 3 } ＞ - 3 ＞ - 4$，所以填“$+$”时，计算结果最大．故选A．

10. 对幻方的研究体现了我国古人的智慧,一个幻方的图案如图1所示,其中9个格中的点数分别为1,2,3,4,5,6,7,8,9,每一横行、每一竖列、每一斜对角线上的点数的和都是15.一个没有填完整的幻方如图2所示,如果它处于同一横行、同一竖列、同一斜对角线上的3个数的和都相等,那么正中间方格中的数为(B)

A.$5$
B.$1$
C.$0$
D.$-1$

答案： 10.B 解析因为同一横行、同一竖列、同一斜对角线上的3个数的和都相等，所以$0 + ( - 1 ) =$正中间方格中的数$+ ( - 2 )$，所以正中间方格中的数为1．

11. 化简:$-\frac{-54}{8}=$$\frac{27}{4}$.

答案： 11.$\frac { 2 7 } { 4 }$ 解析$- \frac { 5 4 } { - 8 } = \frac { 5 4 } { 8 } = \frac { 2 7 } { 4 }$．

12. 一个数是$3.5$,另一个数是$5\frac{1}{2}$的相反数,这两个数的积是$-\frac{77}{4}$.

答案： 12.$- \frac { 7 7 } { 4 }$ 解析$3 . 5 × ( - 5 \frac { 1 } { 2 } ) = - \frac { 7 } { 2 } × \frac { 1 1 } { 2 } = - \frac { 7 7 } { 4 }$．

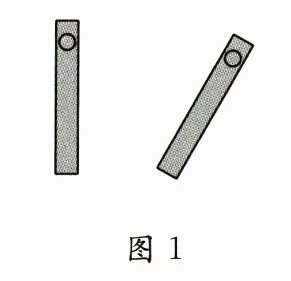
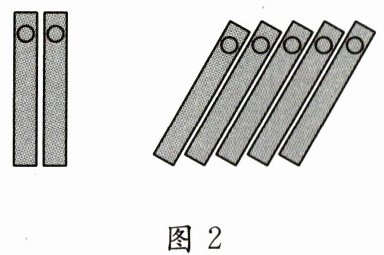
13. 我国古代用算筹(粗细、长短相同的小棍)正放表示正数,斜放表示负数.如图,图1可列式计算为$(+1)+(-1)=0$,由此可推算图2可列的算式为$(+2)+(-5)=-3$.

答案： 13.$( + 2 ) + ( - 5 ) = - 3$ 解析因为算筹正放表示正数，斜放表示负数，所以题图2中可列的算式为$( + 2 ) + ( - 5 ) = - 3$．

14. 某公交车上原有22人,经过3个站点时上、下车情况(上车记为正,下车记为负)如下:$(+3,-7)$,$(+6,-4)$,$(+2,-1)$,则车上还有21人.

答案： 14.21 解析$2 2 + ( - 7 ) + 3 + ( - 4 ) + 6 + ( - 1 ) + 2 = 2 1$（人）．

15. 已知$a,b$都是有理数,若$(a+2)^{2}+|b-1|=0$,则$(a+b)^{2025}=$-1.

答案： 15.$- 1$ 解析因为$( a + 2 ) ^ { 2 } + | b - 1 | = 0$，所以$a + 2 = 0$，$b - 1 = 0$，可得$a = - 2$，$b = 1$，故$( a + b ) ^ { 2 0 2 5 } = ( - 1 ) ^ { 2 0 2 5 } = - 1$．

16. 观察下列各式:$3^{1}=3$,$3^{2}=9$,$3^{3}=27$,$3^{4}=81$,$3^{5}=243$,$3^{6}=729\cdots$你能从中发现底数为3的幂的个位数有什么规律吗?根据你发现的规律回
答:$3^{1010}$的个位数字是9.

答案： 16.9 解析观察题中各式，可得指数为1,2,3,4,5,6$\cdots$时，底数为3的幂的个位数依次为3,9,7,1,3,9$\cdots$，4个数字一循环．$1 0 1 0 ÷ 4 = 2 5 2 \cdots \cdots 2$，故$3 ^ { 1 0 1 0 }$的个位数字是9．