《2025年学习目标与检测同步测试卷七年级数学上册人教版》

19. (8分) 已知一个三角形的第一条边长为$2a + 5b$，第二条边比第一条边长$3a - 2b$，第三条边比第二条边短$3a$.
(1) 用含$a,b$的式子表示这个三角形的周长，并化简；
(2) 若$a,b$满足$|a - 5|+(b - 3)^{2}=0$，求这个三角形的周长.

答案： 19.解
(1)因为三角形的第一条边长为$2a+5b$，第二条边比第一条边长$3a-2b$，第三条边比第二条边短$3a$，所以第二条边长为$2a+5b+3a-2b=5a+3b$，第三条边长为$5a+3b-3a=2a+3b$，
所以这个三角形的周长为$2a+5b+5a+3b+2a+3b=9a+11b$.
(2)因为$a,b$满足$\vert a-5\vert+(b-3)^{2}=0$，
所以$a-5=0,b-3=0$，
所以$a=5,b=3$,所以$9a+11b=9×5+11×3=45+33=78$.
经检验，符合题意.故这个三角形的周长为78.

20. (8分) 已知代数式$A = 3x^{2}-x + 1$，小虎同学在做整式加减运算时，误将“$A - B$”看成“$A + B$”，计算的结果是$2x^{2}-3x - 2$.
(1) 请你帮小虎同学计算出$A - B$的正确结果；
(2) 将$x = -1$代入(1)中的结果并求值.

答案： 20.解
(1)根据题意得，$A=3x^{2}-x+1,A+B$的结果是$2x^{2}-3x-2$，
所以$B=2x^{2}-3x-2-(3x^{2}-x+1)=2x^{2}-3x-2-3x^{2}+x-1=-x^{2}-2x-3$.
所以$A-B=(3x^{2}-x+1)-(-x^{2}-2x-3)=3x^{2}-x+1+x^{2}+2x+3=4x^{2}+x+4$.
(2)当$x=-1$时，原式$=4×(-1)^{2}-1+4=4-1+4=7$.

21. (10分) 某款手机后置摄像头模组如图所示，其中大圆的半径为$r$，中间小圆的半径为$\frac{1}{2}r$，4个半径为$\frac{1}{5}r$的高清圆形镜头分布在两圆之间.

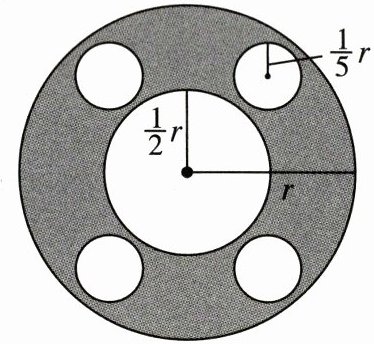
(1) 请用含$r$的式子表示图中阴影部分的面积.
(2) 当$r = 2\mathrm{cm}$时，求图中阴影部分的面积.（$\pi$取3）

答案： 21.解
(1)$\pi r^{2}-\pi×(\frac{1}{2}r)^{2}-\pi×(\frac{1}{5}r)^{2}×4=\frac{59}{100}\pi r^{2}$.
(2)当$r=2cm,\pi$取3时，原式$=\frac{59}{100}×3×2^{2}=\frac{177}{25}(cm^{2})$.