第2页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
10. 如图,圆的周长为4个单位长度,在圆周的4等分点处依次标上数字1,2,3,4,先让圆周上数字1所对应的点与数轴上的数字2所对应的点重合,再让圆沿着数轴向左不滑动的滚动,数轴上的数字$-2024$所对应的点与圆周上重合的点所对应的数字为(
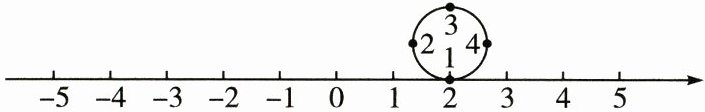
A.1
B.2
C.3
D.4
C
)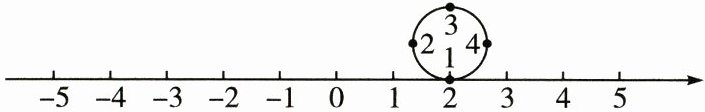
A.1
B.2
C.3
D.4
答案:
10.C 解析 由题意得,圆滚动一周,将沿着数轴滚动$4$个单位长度,因为$(2 + | -2024|)÷4 = 2026÷4 = 506\cdots\cdots2$,所以数轴上的数字$-2024$所对应的点与圆周上的数字$3$所对应的点重合.故选C.
11. 某蓄水池的标准水位记作0m,如果水面高于标准水位0.23m记作$+0.23m$,那么水面低于标准水位0.1m记作
-0.1
m.
答案:
11.$-0.1$ 解析“正”和“负”相对,所以,如果高于标准水位$0.23\ m$,记作$+0.23\ m$,那么低于标准水位$0.1\ m$,应记作$-0.1\ m$.
12. 按规定,食品包装袋上都应标明袋内装有食品多少克,下表是几种饼干的检验结果(单位:g,超过标准质量的记为正数,低于标准质量的记为负数),用绝对值判断最符合标准的一种食品是

甜味
饼干.
答案:
12.甜味 解析 根据题意可知绝对值越小的越接近标准食品,所以甜味饼干是最符合标准的食品.
13. 若$-x=2$,则$-[-(-x)]=$
2
.
答案:
13.2 解析 因为$-x = 2$,所以$-[-(-x)] = -(-2)=2$.
14. 已知$x$是正整数,且$\frac{x}{14}$是假分数,$\frac{x}{16}$是真分数,则$x=$
14或15
.
答案:
14.14或15 解析 根据题意得$x$大于或等于$14$,且小于$16$,因为$x$是正整数,所以$x = 14$或$x = 15$.
15. 若$|x-2|+\left|y-\frac{2}{3}\right|=0$,则$x=$
2
,$y=$\frac{2}{3}
.
答案:
15.$2,\frac{2}{3}$ 解析 根据题意可得,$x - 2 = 0,y - \frac{2}{3}=0$,解得$x = 2,y = \frac{2}{3}$.
16. 数轴上,若点$A$和点$B$分别表示互为相反数的两个数,点$A$在点$B$的左侧,并且这两点之间的距离是16.若数轴上点$C$距离点$B$9个单位长度,则点$C$所表示的数是
17或-1
.
答案:
16.17或$-1$ 解析 由题意可得,点$B$表示的数为$8$.当点$C$在点$B$的右侧,且距离$9$个单位长度时,点$C$表示的数是$17$;当点$C$在点$B$的左侧,且距离$9$个单位长度时,点$C$表示的数是$-1$.故点$C$所表示的数是$17$或$-1$.
17. (8分)所有正有理数组成正有理数集合,所有负有理数组成负有理数集合.把下面的有理数填入它们属于的集合内.
$-11,-\frac{3}{5},-9,0.5,+12,-6.4,2.\dot{2},-4\%$.
(1)正有理数集合:{ …}.
(2)负有理数集合:{ …}.
$-11,-\frac{3}{5},-9,0.5,+12,-6.4,2.\dot{2},-4\%$.
(1)正有理数集合:{ …}.
(2)负有理数集合:{ …}.
答案:
17.解
(1)正有理数集合:$\{0.5, +12,2.2\cdots\}$;
(2)负有理数集合:$\{-11,-\frac{3}{5},-9,-6.4,-4\%\cdots\}$.
(1)正有理数集合:$\{0.5, +12,2.2\cdots\}$;
(2)负有理数集合:$\{-11,-\frac{3}{5},-9,-6.4,-4\%\cdots\}$.
18. (8分)画一条数轴,把$-3,4,-2\frac{1}{2},1.5$这四个数在数轴上表示出来,并用“$<$”连接.
答案:
18.解 如图,

所以$-3 < -2\frac{1}{2} < 1.5 < 4$.
18.解 如图,

所以$-3 < -2\frac{1}{2} < 1.5 < 4$.
查看更多完整答案,请扫码查看


