《2025年学习目标与检测同步测试卷七年级数学上册人教版》

10. 已知M = -2a² + 4a + 1，N = -3a² + 4a - 1，则M与N的大小关系是(A)

A.M ＞ N
B.M ＜ N
C.M = N
D.以上都有可能

答案： 10. A 解析 因为$M-N=-2a^{2}+4a+1-(-3a^{2}+4a-1)=-2a^{2}+4a+1+3a^{2}-4a+1=a^{2}+2＞0$，所以$M＞N$.故选A.

11. 在代数式①$\frac{x + y}{x}$，②$\frac{x^{5} + y^{3}}{2}$，③0.25m²n⁴，④4021，⑤1 + $\frac{3}{x}$，⑥$\frac{2}{\pi}$中，是整式的有②③④⑥.(填序号)

答案： 11. ②③④⑥

12. 已知多项式$(m - 2)x^{|m|} + mx - 3$的次数为2，则m = -2.

答案： 12. $-2$ 解析 因为多项式$(m-2)x^{|m|}+mx-3$的次数为2，所以$m-2$的值不为0，且$|m|=2$，所以$m=-2$.

13. 老师在黑板上书写了一个正确的演算过程，随后用手掌捂住了一个多项式，形式如下：
- 2x² - 2x + 1 = -x² + 5x - 3，则所捂住的多项式是x²+7x-4.

答案： 13. $x^{2}+7x-4$ 解析 所捂住的多项式是$-x^{2}+5x-3+2x^{2}+2x-1=x^{2}+7x-4$.

14. 已知m + n = -2，mn = -4，则3(2m - mn) - 2(mn - 3n)的值为8.

答案： 14. 8 解析 原式$=6m-3mn-2mn+6n=6(m+n)-5mn$，当$m+n=-2,mn=-4$时，原式$=6×(-2)-5×(-4)=8$.

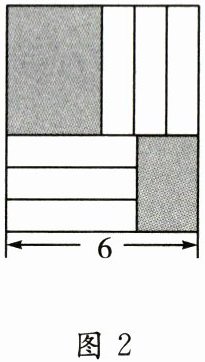
15. 如图，把六张形状大小完全相同的小长方形卡片(如图1，长为a，宽为b)不重叠地放在一个底面为长方形的盒子底部(如图2)，盒子底面未被卡片覆盖的部分用阴影表示，则图2中两块阴影部分的周长和是24.

答案： 15. 24 解析 由题意可得，题图2中两块阴影部分的周长和为$2a+(6-3b)×2+3b×2+(6-a)×2=2a+12-6b+6b+12-2a=24$.

16. 如果整式A与整式B的和为有理数a，我们称A，B为a的“友好整式”，例如：x - 4与-x + 5为1的“友好整式”；2ab + 3与-2ab + 4为7的“友好整式”.若关于x的整式2x² + 3x + 6与-2x² - 3x + 2为n的“友好整式”，则n的值为8.

答案： 16. 8 解析 由题意可知，$n=(2x^{2}+3x+6)+(-2x^{2}-3x+2)=2x^{2}+3x+6-2x^{2}-3x+2=6+2=8$.

17. （8分）计算：
（1）4(-3a² - ab) - 2(5ab - 8b²)；
（2）$\frac{2}{3}(6x^{2} - 3x^{2}y) - [2xy + (-2x^{2}y + 3x^{2}) - \frac{1}{2}xy^{2}]$.

答案： 17. 解
(1)原式$=-12a^{2}-4ab-10ab+16b^{2}=-12a^{2}-14ab+16b^{2}$.
(2)原式$=4x^{2}-2x^{2} y-(2xy-2x^{2} y+3x^{2}-\frac{1}{2}xy^{2})=4x^{2}-2x^{2} y-2xy+2x^{2} y-3x^{2}+\frac{1}{2}xy^{2}=x^{2}-2xy+\frac{1}{2}xy^{2}$.