《2025年学习目标与检测同步测试卷七年级数学上册人教版》

7. 足球比赛的记分为胜一场得3分，平一场得1分，负一场得0分，一队打了14场比赛，负5场，共得19分，那么这个队的胜场数是(B)

A.3
B.5
C.7
D.9

答案： 7.B 解析 设胜场数为$x$，则平了$(14 - 5 - x)$场，由题意，得$3x + (14 - 5 - x) = 19$，解得$x = 5$.故选 B.

8. 一项工程甲单独做需要40天完成，乙单独做需要50天完成，甲先单独做4天，然后两人合作$x$天完成这项工程，则可列的方程是(D)

A.$\frac{x}{40}+\frac{x}{40 + 50}=1$
B.$\frac{4}{40}+\frac{x}{40×50}=1$
C.$\frac{4}{40}+\frac{x}{50}=1$
D.$\frac{4}{40}+\frac{x}{40}+\frac{x}{50}=1$

答案： 8.D

9. 一个正两位数，个位数字与十位数字的和是9，如果将个位数字与十位数字对调后所得的新数比原数大9，则原来的两位数为(D)

A.54
B.27
C.72
D.45

答案： 9.D 解析 设原数的个位数字是$x$，则十位数字是$9 - x$.根据题意得，$10x + (9 - x) = 10(9 - x) + x + 9$，解得$x = 5$，$9 - 5 = 4$，则原来的两位数为$45$.故选 D.

10. 某书店推出售书优惠方案：①一次性购书不超过100元，不享受优惠；②一次性购书超过100元，但不超过200元，一律打九折；③一次性购书超过200元，一律打八折.若小明同学一次性购书付款162元，则他所购书的原价为(C)

A.180元
B.202.5元
C.180元或202.5元
D.180元或200元

答案： 10.C 解析 因为$200 × 0.9 = 180$（元），$200 × 0.8 = 160$（元），$160 ＜ 162 ＜ 180$，所以小明同学一次性购书付款$162$元，可能有两种情况.使用优惠方案②时，$162 ÷ 0.9 = 180$（元）；使用优惠方案③时，$162 ÷ 0.8 = 202.5$（元），所以他所购书的原价为$180$元或$202.5$元.故选 C.

11. 关于$x$的方程$3x - 8 = x$的解为x = 4.

答案： 11.$x = 4$

12. 小华和小明周末去骑行.他们按设计好的同一条线路同时出发，小华每小时骑行18km，小明每小时骑行12km，骑完全程，小明所用的时间比小华多半小时.设他们这次骑行的线路长为$x$km，依题意，可列方程为$\frac{x}{18} + \frac{1}{2} = \frac{x}{12}$.

答案： 12.$\frac{x}{18} + \frac{1}{2} = \frac{x}{12}$

13. 小刚在解方程$x = 1-\frac{x - ●}{5}$时，不小心把一个数字用墨水污染了，他翻阅了答案知道这个方程的解为$x = 1$，于是他判断●应该是1.

答案：
13.1 解析 用$a$表示，把$x = 1$代入方程得$1 = 1 - \frac{1 - a}{5}$，解得$a = 1$.故 应该是$1$.

14. 现规定一种新的运算$\begin{vmatrix}a&b\\c&d\end{vmatrix}=ad - bc$($a$，$b$，$c$，$d$为有理数)，则满足$\begin{vmatrix}\frac{x}{2}&\frac{x + 1}{3}\\2&-1\end{vmatrix}=1$的$x$的值为$-\frac{10}{7}$.

答案： 14.$-\frac{10}{7}$ 解析 由题意可得，$\frac{x}{2} × (-1) - 2 × \frac{x + 1}{3} = 1$，解得$x = -\frac{10}{7}$.

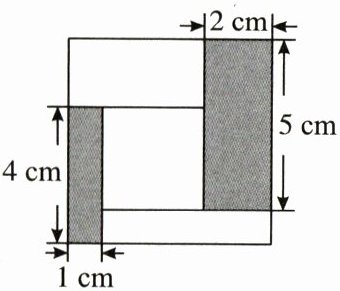
15. 如图，用一块长5cm、宽2cm的长方形纸板，和一块长4cm、宽1cm的长方形纸板，与一块正方形纸板以及另两块长方形纸板，恰好拼成一个大正方形，则拼成的大正方形的面积是36$cm^{2}$.

答案： 15.$36$ 解析 设题图中正方形纸板的边长为$x cm$，则大正方形的边长为$[4 + (5 - x)] cm$或$(x + 1 + 2) cm$，所以$4 + (5 - x) = x + 1 + 2$，解得$x = 3$，$3 + 1 + 2 = 6( cm)$，所以大正方形的面积为$6^2 = 36( cm^2)$.

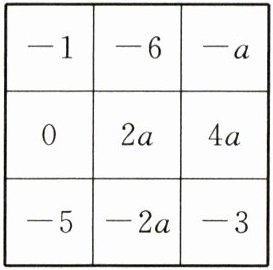
16. 幻方最早源于我国，古人称之为纵横图.如图，该幻方的各行、各列及各条对角线上的三个数字之和均相等，则图中$a$的值为-1.

答案： 16.$-1$ 解析 根据题意得，$-1 - 6 - a = -1 + 0 - 5$，解得$a = -1$，故图中$a$的值为$-1$.