《2025年学习目标与检测同步测试卷七年级数学上册人教版》

9. 若$|a|=a$,则数$a$在数轴上的对应点在(D)

A.原点左侧
B.原点或原点左侧
C.原点右侧
D.原点或原点右侧

答案： 9.D 解析 因为$\vert a\vert=a$,所以$a$一定是非负数,所以数$a$在数轴上的对应点一定在原点或原点右侧.故选D.

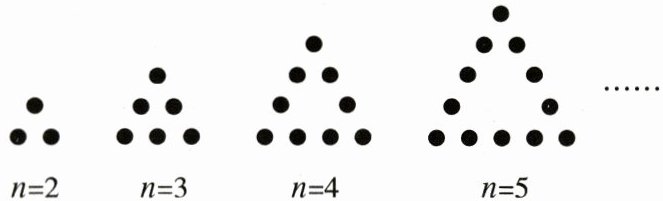
10. 如图,由一些点组成形如三角形的图形,每条“边”(包括两个顶点)有$n(n＞1)$个点,记第$1$个图形中总的点数为$S_{2}=3$,第$2$个图形中总的点数为$S_{3}=6$,第$3$个图形中总的点数为$S_{4}=9$,第$4$个图形中总的点数为$S_{5}=12, \cdots \cdots$依此类推,则$S_{2025}$的值是(C)


A.$6066$
B.$6069$
C.$6072$
D.$6075$

答案： 10.C 解析 第1个图形中总的点数为$S_2=3=3×(2 - 1)$;第2个图形中总的点数为$S_3=6=3×(3 - 1)$;第3个图形中总的点数为$S_4=9=3×(4 - 1)$;第4个图形中总的点数为$S_5=12=3×(5 - 1)\cdots\cdots$以此类推,第$n$个图形中总的点数为$S_{n + 1}=3×(n + 1 - 1)=3n$,所以$S_{2025}=3×(2025 - 1)=6072$.故选C.

11. 近年来,我国科技工作者践行“科技强国”使命,不断取得世界级的科技成果.如由我国研制的中国首台作业型全海深自主遥控潜水器“海斗一号”,最大下潜深度$10907$米,填补了中国水下万米作业型无人潜水器的空白;由我国自主研发的极目一号Ⅲ型浮空艇“大白鲸”,升空高度至海拔$9050$米,创造了浮空艇原位大气科学观测海拔最高的世界纪录.如果把海平面以上$9050$米记作$+9050$米,那么海平面以下$10907$米记作-10907米.

答案： 11.$-10907$米

12. 比较大小:$-2$＜$+6$;$-\frac{1}{3}$＞$-\frac{1}{2}$;$-|-1|$＜$-(-1)$.(填“$＞$”或“$＜$”)

答案： 12.$＜ ＞ ＜$

13. 有理数$5.6149$精确到百分位的近似数为5.61.

答案： 13.$5.61$

14. 已知$x-3=2$,则代数式$(x-3)^{2}-2(x-3)+1$的值为1.

答案： 14.$1$ 解析 由题意可得,原式$=2^2 - 2×2 + 1 = 1$.

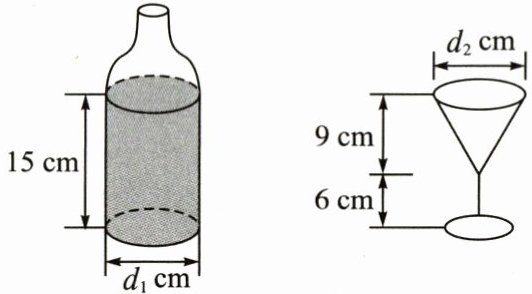
15. 一个装了一些果汁的瓶子和一个圆锥形玻璃杯如图所示,且$d_{1}=d_{2}$.如果把瓶子中的果汁全部倒人这个圆锥形玻璃杯中,最多可以倒满5杯.(瓶子和玻璃杯的壁厚忽略不计)

答案： 15.$5$ 解析 瓶子内含有的果汁的体积为$V_1=\pi×(\frac{d_1}{2})^2×15 = 15\pi×(\frac{d_1}{2})^2(cm^3)$,一个圆锥形玻璃杯最多能装液体的体积为$V_2=\frac{1}{3}\pi×(\frac{d_2}{2})^2×9 = 3\pi×(\frac{d_2}{2})^2(cm^3)$,因为$d_1 = d_2$,所以$V_1 = 5V_2$,所以最多可以倒满$5$杯.

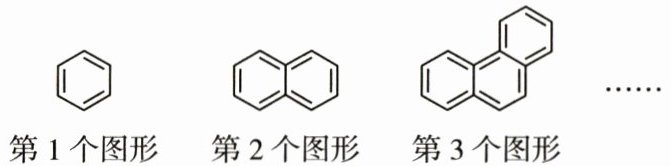
16. 苯是一种石油化工基本原料,其产量和生产的技术水平是一个国家石油化工发展水平的标志之一.如图,小明用$9$根木棒搭建的第$1$个图形就是类似于苯的结构简式,他继续用木棒搭建与苯有关联的各个图形,按此规律,搭建第$n$($n$为正整数)个图形所需木棒的根数为8n+1.

答案： 16.$8n + 1$ 解析 因为第1个图形所需木棒的根数为$9 = 8×1 + 1$,第2个图形所需木棒的根数为$17 = 8×2 + 1$,第3个图形所需木棒的根数为$25 = 8×3 + 1\cdots\cdots$所以第$n$个图形所需木棒的根数为$8n + 1$.