第68页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
21. (10 分)如图,$C$ 为线段 $AD$ 上一点,$B$ 为线段 $CD$ 的中点,且 $AD = 8$ cm,$BD = 2$ cm.
(1)图中共有
(2)求线段 $AC$ 的长;
(3)若点 $E$ 在直线 $AD$ 上,且 $EA = 3$ cm,求线段 $BE$ 的长.
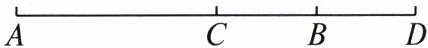
(1)图中共有
6
条线段;(2)求线段 $AC$ 的长;
(3)若点 $E$ 在直线 $AD$ 上,且 $EA = 3$ cm,求线段 $BE$ 的长.
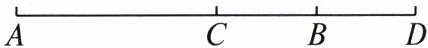
答案:
21.解(1)6
(2)因为B为线段CD的中点,所以CD = 2BD.
因为BD = 2cm,所以CD = 4cm.
因为AC = AD - CD且AD = 8cm,CD = 4cm,所以AC = 4cm.
(3)当点E在点A的左侧时,BE = BA + EA,因为BA = 6cm,EA = 3cm,所以BE = 9cm;
当点E在点A的右侧时,BE = BA - EA,因为BA = 6cm,EA = 3cm,所以BE = 3cm.
综上,线段BE的长为3cm或9cm.
(2)因为B为线段CD的中点,所以CD = 2BD.
因为BD = 2cm,所以CD = 4cm.
因为AC = AD - CD且AD = 8cm,CD = 4cm,所以AC = 4cm.
(3)当点E在点A的左侧时,BE = BA + EA,因为BA = 6cm,EA = 3cm,所以BE = 9cm;
当点E在点A的右侧时,BE = BA - EA,因为BA = 6cm,EA = 3cm,所以BE = 3cm.
综上,线段BE的长为3cm或9cm.
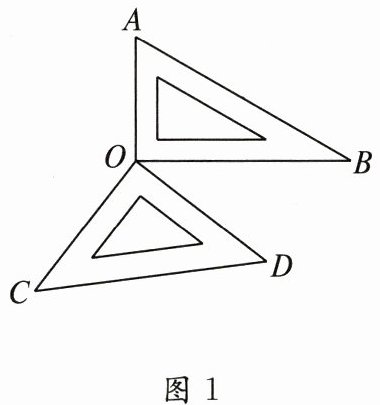
22. (12 分)如图 1,将一副三角尺的直角顶点重合在点 $O$ 处.
(1)①探究$\angle AOD$与$\angle BOC$的关系:
因为$\angle AOB = \angle COD = 90^{\circ}$,
所以$\angle AOB +$
即$\angle AOD$
②探究$\angle AOC$与$\angle BOD$的关系:
因为$\angle AOB = \angle COD = 90^{\circ}$,$\angle AOC + \angle AOB + \angle BOD + \angle COD = 360^{\circ}$,
所以$\angle AOC + \angle BOD =$
即$\angle AOC$与$\angle BOD$的关系为
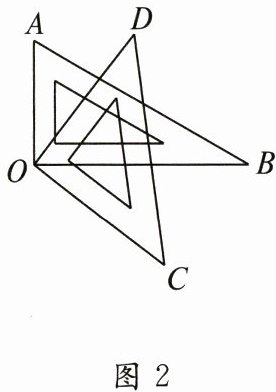
(2)若将等腰的三角尺绕点 $O$ 旋转到如图 2 所示的位置.
①$\angle AOD$和$\angle BOC$相等吗?说明理由(仿照上面,写出推理过程).
②$\angle AOC$和$\angle BOD$的以上关系还成立吗?说明理由(仿照上面,写出推理过程).
(1)①探究$\angle AOD$与$\angle BOC$的关系:
因为$\angle AOB = \angle COD = 90^{\circ}$,
所以$\angle AOB +$
∠BOD
$= \angle COD +$∠BOD
,即$\angle AOD$
=
$\angle BOC$.②探究$\angle AOC$与$\angle BOD$的关系:
因为$\angle AOB = \angle COD = 90^{\circ}$,$\angle AOC + \angle AOB + \angle BOD + \angle COD = 360^{\circ}$,
所以$\angle AOC + \angle BOD =$
180°
.即$\angle AOC$与$\angle BOD$的关系为
互补
.(2)若将等腰的三角尺绕点 $O$ 旋转到如图 2 所示的位置.
①$\angle AOD$和$\angle BOC$相等吗?说明理由(仿照上面,写出推理过程).
②$\angle AOC$和$\angle BOD$的以上关系还成立吗?说明理由(仿照上面,写出推理过程).


答案:
22.解(1)①因为∠AOB = ∠COD = 90°,
所以∠AOB + ∠BOD = ∠COD + ∠BOD,
即∠AOD = ∠BOC.
故答案为∠BOD,∠BOD,=.
②因为∠AOB = ∠COD = 90°,∠AOC + ∠AOB + ∠BOD + ∠COD = 360°,所以∠AOC + ∠BOD = 180°,
即∠AOC与∠BOD的关系为互补.
故答案为180°,互补.
(2)①相等.理由:因为∠AOB = ∠COD = 90°,
所以∠AOB - ∠BOD = ∠COD - ∠BOD,
即∠AOD = ∠BOC.
②成立.理由:因为∠AOB = ∠COD = 90°,
所以∠AOB + ∠BOC + ∠BOD = 180°.
即∠AOC + ∠BOD = 180°,
所以∠AOC与∠BOD的关系为互补.
所以∠AOB + ∠BOD = ∠COD + ∠BOD,
即∠AOD = ∠BOC.
故答案为∠BOD,∠BOD,=.
②因为∠AOB = ∠COD = 90°,∠AOC + ∠AOB + ∠BOD + ∠COD = 360°,所以∠AOC + ∠BOD = 180°,
即∠AOC与∠BOD的关系为互补.
故答案为180°,互补.
(2)①相等.理由:因为∠AOB = ∠COD = 90°,
所以∠AOB - ∠BOD = ∠COD - ∠BOD,
即∠AOD = ∠BOC.
②成立.理由:因为∠AOB = ∠COD = 90°,
所以∠AOB + ∠BOC + ∠BOD = 180°.
即∠AOC + ∠BOD = 180°,
所以∠AOC与∠BOD的关系为互补.
查看更多完整答案,请扫码查看


