《2025年名校课堂七年级数学上册人教版贵州专版》

9. 计算：$-2^{2}× \frac{1}{4}÷ (-\frac{1}{2})^{2}× (-2)^{3}$.

答案： 9.解:原式$=-4×\frac {1}{4}÷\frac {1}{4}×(-8)=4×\frac {1}{4}×4×8=32.$

10. (2024·甘肃)定义一种新运算“$*$”,规定运算法则为$m*n = m^{n}-mn$($m$,$n$均为整数,且$m\neq 0$).例如：$2*3 = 2^{3}-2× 3 = 2$.则$(-2)*2= \underline{\quad\quad}$8.

答案： 10.8

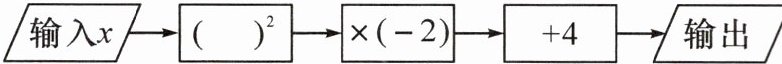
11. 如图,这是一个简单的数值运算程序.当输入$x的值为-1$时,输出的数值为$\underline{2}$.

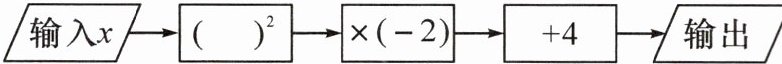
答案： 11.2

12. (2024·黔东南期末)我们平常用的数是十进制的数,如：$1234 = 1× 10^{3}+2× 10^{2}+3× 10^{1}+4× 10^{0}$.表示十进制的数要用十个数码：$0$,$1$,$2$,$3$,$4$,$5$,$6$,$7$,$8$,$9$.在电子计算机中用的是二进制,只用两个数码$0和1$.如：二进制中,$101 = 1× 2^{2}+0× 2^{1}+1× 2^{0}$,等于十进制的数$5$；$10111 = 1× 2^{4}+0× 2^{3}+1× 2^{2}+1× 2^{1}+1× 2^{0}$,等于十进制的数$23$.则二进制中的$110010等于十进制的数\underline{\quad\quad}$.(规定：当$a\neq 0$时,$a^{0}= 1$)
50

答案： 12.50

13. 计算：
(1) $-1^{2}-(1-\frac{1}{3})÷ 3× (-\frac{3}{2})^{2}$.
(2) $-2^{4}+\vert - 5\vert -[-(-3)÷ \frac{1}{6}+2]$.

答案： 13.解:
(1)原式$=-1-\frac {2}{3}×\frac {1}{3}×\frac {9}{4}=-1-\frac {1}{2}=-1\frac {1}{2}.$
(2)原式$=-16+5-(3×6+2)=-16+5-20=-31.$

14. (2024·黔东南第四中学期中)已知有理数$a$,$b$互为相反数,$c$,$d$互为倒数,有理数$m和-2在数轴上表示的点相距3$个单位长度,求$\vert m\vert+\frac{a + b}{2024}+(-cd)^{2025}$的值.

答案： 14.解:根据题意,得$a+b=0,cd=1,m=-5$或$m=1$.①当$m=-5$时,原式$=|-5|+0-1=5-1=4$;②当$m=1$时,原式$=|1|+0-1=1-1=0$.所以$|m|+\frac {a+b}{2024}+(-cd)^{2025}$的值为4或0.

15. 新考向 推理能力观察下面三行数：
$2$,$-4$,$8$,$-16$,…$$；①
$-1$,$2$,$-4$,$8$,…$$；②
$3$,$-3$,$9$,$-15$,…$$.③
(1) 第①行的数按如下规律排列：
$2^{1}$,$\underline{$-2^{2}$}$,$\underline{$2^{3}$}$,$\underline{$-2^{4}$}$,…$$.
(2) 第②③行的数与第①行的数分别有什么关系？
(3) 取每行数的第$9$个数,计算这三个数的和.
(2)第②行的数是由第①行相应的数除以-2得到的;第③行的数是由第①行相应的数加1得到的.
(3)$2^{9}+2^{9}÷(-2)+2^{9}+1=2^{9}+2^{9}×(-\frac {1}{2})+2^{9}+1=512+(-256)+512+1=769.$

答案： 15.解:
(1)$-2^{2}$ $2^{3}$ $-2^{4}$
(2)第②行的数是由第①行相应的数除以-2得到的;第③行的数是由第①行相应的数加1得到的.
(3)$2^{9}+2^{9}÷(-2)+2^{9}+1=2^{9}+2^{9}×(-\frac {1}{2})+2^{9}+1=512+(-256)+512+1=769.$