《2025年名校课堂七年级数学上册人教版贵州专版》

9. 若数轴上表示$-1和3的两点分别是点A和点B$,则点$A和点B$之间的距离是(D)
A.$-4$
B.$-2$
C.$2$
D.$4$

答案： D

10. 能与$-(\frac{3}{4} - \frac{6}{5})$相加得0的是(C)
A.$- \frac{3}{4} - \frac{6}{5}$
B.$\frac{6}{5} + \frac{3}{4}$
C.$- \frac{6}{5} + \frac{3}{4}$
D.$- \frac{3}{4} + \frac{6}{5}$

答案： C

11. (2024·黔东南台江一中期中)当输入的值为$-1$时,按如图所示的程序运算,则输出的是(A)
A.$1$
B.$3$
C.$-5$
D.$5$

答案： A

12. 数学活动中,王老师给同学们出了一道题：规定一种新运算“★”,对于任意有理数$a和b$,有$a★b = a - b + 1$. 请根据新运算,计算$(2★3)★2$的值是(B)
A.$0$
B.$-1$
C.$-2$
D.$1$

答案： B

13. 计算：$(-9 \frac{1}{3}) - | - 4 \frac{5}{6}| + |0 - 5 \frac{1}{6}| - \frac{2}{3}$.

答案： 13.解:原式=$-9\frac{1}{3}-4\frac{5}{6}+5\frac{1}{6}-\frac{2}{3}=(-9\frac{1}{3}-\frac{2}{3})+(-4\frac{5}{6}+5\frac{1}{6})=-10+\frac{1}{3}=-9\frac{2}{3}$.

14. 一天上午,一辆警车从$M$车站出发在一条笔直的公路上来回巡逻,行驶的路程情况如下(向$M$车站右侧方向行驶记为正,单位：$km$).
$-7$,$+4$,$+8$,$-3$,$+10$,$-3$,$-6$,$-12$,$+9$,$-3$.
(1) 这辆警车在完成上述来回巡逻后在$M$车站的哪一侧,距$M$车站多少千米？
(2) 如果这辆警车每行驶$100 km的耗油量为11 L$,这天上午共消耗汽油多少升？

答案： 14.解:
(1)-7+4+8-3+10-3-6-12+9-3=(4+8+10+9)-(7+3+3+6+12+3)=31-34=-3(km).答:这辆警车在完成上述来回巡逻后在M车站的左侧,距M车站3 km.
(2)$(| -7|+| +4|+| +8|+| -3|+| +10|+| -3|+| -6|+| -１２|+| +９|+| -３|)×\frac{11}{1００}=(7+4+8+３+１０+３+６+１２+９+３)×\frac{１１}{１００}=６５×\frac{１１}{１００}=７.１５$(L).答:这天上午共消耗汽油7.15 L.

15. 已知$A$,$B两点在数轴上表示的数分别为m$,$n$.
(1) 对照数轴填写下表：

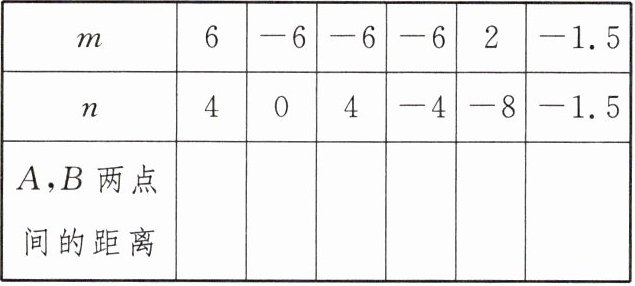
(2) 若$A$,$B两点间的距离记为d$,试问$d与m$,$n$有何等量关系？并用文字描述出来.
(3) 已知$A$,$B两点在数轴上表示的数分别为x$,$-1$,则$A$,$B两点间的距离d$可表示为______；如果$d = 3$,求$x$的值.
(1)２　６　１０　２　１０　０
(2)$d=|m-n|$.数轴上两点之间的距离,等于这两点在数轴上对应的数の差の绝对值.
(3)$|x+1|$　当$d=３$时,$|x+１|=３$,$\therefore x=２$或$-４$.

答案： 15.解:
(1)２　６　１０　２　１０　０　
(2)$d=|m-n|$.数轴上两点之间的距离,等于这两点在数轴上对应的数の差の绝对值.
(3)$|x+1|$　当$d=３$时,$|x+１|=３$,$\therefore x=２$或$-４$.