《2025年名校课堂七年级数学上册人教版贵州专版》

9. 计算：
(1) $(-32\frac{16}{25})÷(-8×4)$.
(2) $\frac{7}{3}×|\frac{1}{6}-\frac{1}{3}|×\frac{3}{14}÷(-\frac{3}{8})$.

答案： 解:
(1)原式$=(-32\frac{16}{25})÷(-32)=(32+\frac{16}{25})×\frac{1}{32}=32×\frac{1}{32}+\frac{16}{25}×\frac{1}{32}=1\frac{1}{50}.(2)$原式$=\frac{7}{3}×\frac{1}{6}×\frac{3}{14}×(-\frac{8}{3})=-\frac{2}{9}.$

10. 某盲盒专卖店以 $20$ 元的单价购进一批盲盒,为合理定价,销售第一周试行机动价格,售出时以单价 $25$ 元为标准,超出 $25$ 元的部分记为正,不足 $25$ 元的部分记为负.该店第一周盲盒的售价单价和售出情况如下表所示：

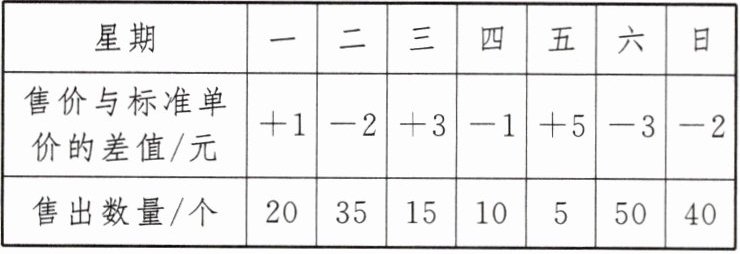
(1) 第一周该店出售这批盲盒,单价最高的是星期 五,最高单价是 30 元.
(2) 第一周该店出售这批盲盒的收益如何？(求盈利或亏损的总价)
解:1×20+(-2)×35+3×15+(-1)×10+5×5+(-3)×50+(-2)×40=-220(元),(25-20)×(20+35+15+10+5+50+40)+(-220)=655(元).
答:第一周该店出售这批盲盒盈利655元.

答案： 解:
(1)五 30
(2)1×20+(-2)×35+3×15+(-1)×10+5×5+(-3)×50+(-2)×40=-220(元),(25-20)×(20+35+15+10+5+50+40)+(-220)=655(元).
答:第一周该店出售这批盲盒盈利655元.

11. A 北师大附属实验校本经典题 有一种“二十四点”的扑克牌游戏,其游戏规则如下：一副扑克牌去掉大王、小王,剩下的每张牌对应一个 $1\sim13$ 之间(包括 $1$ 和 $13$)的整数,任取 $4$ 张扑克牌,得到 $4$ 个对应的整数,将这 $4$ 个整数进行加减乘除运算(每张扑克牌对应的数用且只用一次),使其结果等于 $24$.
例如：对 $1$,$2$,$3$,$4$ 可作运算 $(1 + 2 + 3)×4 = 24$ [注：与 $4×(1 + 2 + 3) = 24$ 视为相同].
现有 $4$ 个数：$3$,$4$,$-6$,$10$,请运用上述的规则写出 $3$ 种不同的算式,使其结果都等于 $24$.

答案： 解:答案不唯一,如:[10+(-6)+4]×3,(10-4)×3-(-6),4-10×(-6)÷3.

微专题 1 “$\frac{a}{|a|}$型”的分类讨论问题
以题明法
分类讨论是一种重要的数学方法.例如,在化简 $|a|$ 时,可以这样分类：
当 $a＞0$ 时,$|a| = a$；
当 $a = 0$ 时,$|a| = 0$；
当 $a＜0$ 时,$|a| = -a$.
请用上述方法解决下列问题：
(1) 当 $a = 5$ 时,$\frac{|a|}{a}= $ ______.
(2) 当 $a = -2$ 时,$\frac{a}{|a|}= $ ______.
(3) 已知 $a$,$b$ 是有理数,当 $ab＞0$ 时,试求 $\frac{a}{|a|}+\frac{|b|}{b}$ 的值.

答案： 解:
(1)1
(2)-1
(3)
∵ab＞0,
∴a,b同为正数或a,b同为负数.①当a,b同为正数,即a＞0,b＞0时,|a|=a,|b|=b,
∴$\frac{a}{|a|}+\frac{|b|}{b}=\frac{a}{a}+\frac{b}{b}=1+1=2；$②当a,b同为负数,即a＜0,b＜0时,|a|=-a,|b|=-b,
∴\frac{a}{|a|}+\frac{|b|}{b}=\frac{a}{-a}+\frac{-b}{b}=-1-1=-2.综上所述,当ab＞0时$,\frac{a}{|a|}+\frac{|b|}{b}$的值为2或-2.

1. 对于有理数 $x$,$y$,若 $xy＜0$,则 $\frac{xy}{|xy|}+\frac{x}{|x|}+\frac{|y|}{y}$ 的值是 (B)
A.$-3$
B.$-1$
C.$1$
D.$3$

答案： B

2. 已知非零有理数 $a$,$b$,$c$ 满足 $\frac{a}{|a|}+\frac{|b|}{b}+\frac{c}{|c|}= -1$,则 $\frac{|abc|}{abc}= $ (D)
A.$\pm1$
B.$-1$
C.$0$
D.$1$

答案： D