《2025年学习之友八年级数学上册人教版》

7. 已知 $x - y = 1$,$xy = 2$,求 $x^3y - 2x^2y^2 + xy^3$ 的值。

答案： 解:$x^{3}y-2x^{2}y^{2}+xy^{3}$
$=xy(x^{2}-2xy+y^{2})$
$=xy(x-y)^{2}$,
当$x-y=1,xy=2$时,原式$=2×1^{2}=2$.

8. 若 $x$,$y$ 互为相反数,且 $(x + 2)^2 - (y + 1)^2 = 4$,求 $x$,$y$ 的值。

答案： 解:
∵x,y 互为相反数且$(x+2)^{2}-(y+1)^{2}=4$,则有$x+y=0,x=-y$,
∴$(x+2+y+1)(x+2-y-1)=4$,
∴$(x+y+3)(x-y+1)=4$,则$3(x-y+1)=4,3(-y-y+1)=4$,
∴$y=-\frac{1}{6},x=\frac{1}{6}$.

9. 试说明：对于任意自然数 $n$,$(n + 7)^2 - (n - 5)^2$ 都能被 $24$ 整除。

答案： 解:$(n+7)^{2}-(n-5)^{2}=24n+24=24(n+1)$,
∴能被 24 整除.

1. 观察规律并填空：


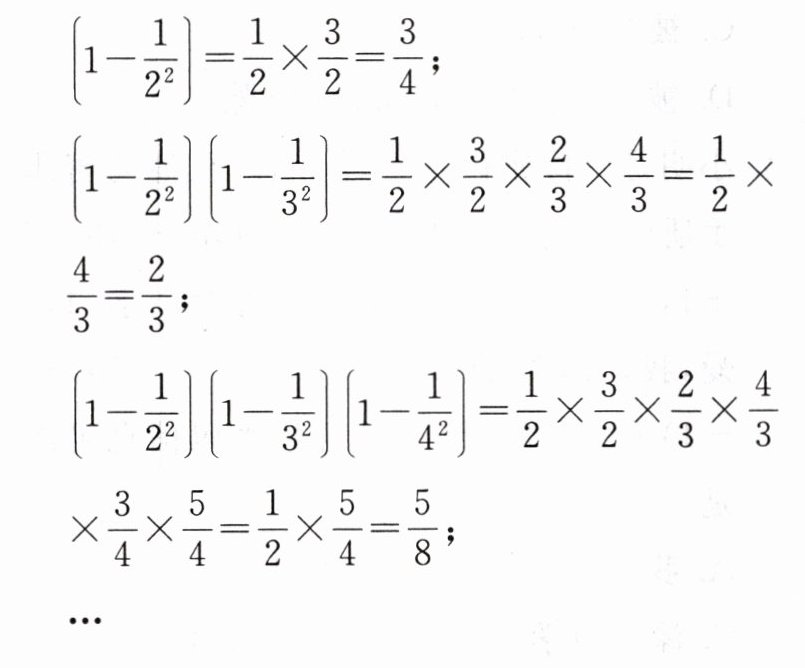
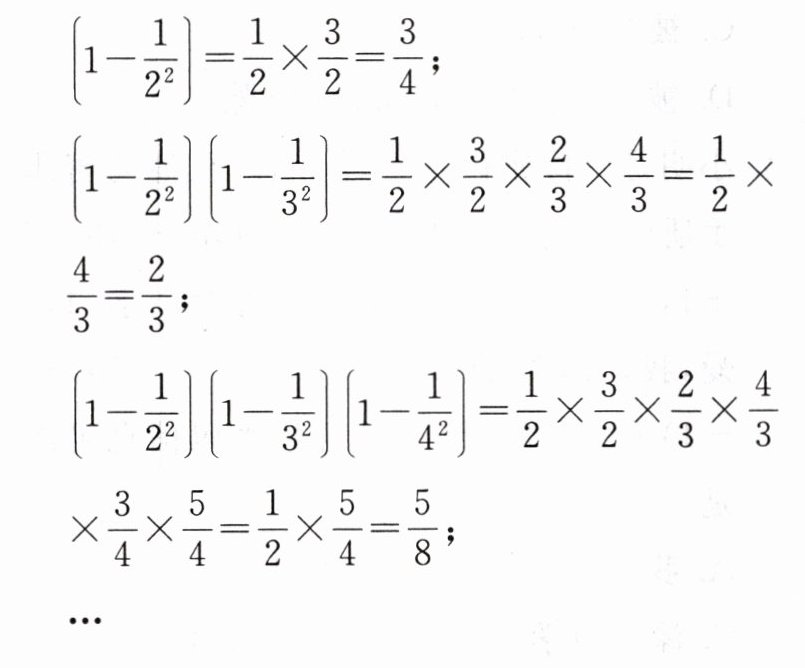
(用含 $n$ 的式子表示,$n$ 是正整数,且 $n \geq 2$)

答案： $\frac{n+1}{2n}$

2. 阅读并解决问题：对于二次三项式 $x^2 + 4x - 12$,因不能直接运用完全平方公式,此时,我们可以在 $x^2 + 4x - 12$ 中先加上一项 $4$,使它与 $x^2 + 4x$ 的和成为一个完全平方式,再减去 $4$,式子的值不变,于是有：$x^2 + 4x - 12 = (x^2 + 4x + 4) - 4 - 12 = (x + 2)^2 - 4^2 = (x + 6)(x - 2)$。像这样,先添一适当项,使式中出现完全平方式,再减去这个项,使整个式子的值不变的方法称为“配方法”。
(1) 利用“配方法”分解因式：$x^2 - 6x + 5$。
(2) 同时运用多项式的配方法能确定一些多项式的最大值或最小值。因为不论 $x$ 取何值,$(x + 2)^2 \geq 0$,所以当 $x = -2$ 时,多项式 $x^2 + 4x - 12$ 有最小值为 $-16$。试确定：多项式 $-x^2 + 2x + 16$ 是否存在最大值或最小值？如果有,请求出最大值或最小值；如果不存在,请说明理由。
(3) 已知 $x$ 是实数,试比较 $x^2 - 4x + 5$ 与 $-x^2 + 4x - 4$ 的大小,说明理由。

答案：
(1)$x^{2}-6x+5=(x^{2}-6x+9)-9+5$
$=(x-3)^{2}-4$
$=(x-3+2)(x-3-2)$
$=(x-1)(x-5)$;
(2)$-x^{2}+2x+16$
$=-(x^{2}-2x+1)+16+1$
$=-(x-1)^{2}+17$;
∵$-(x-1)^{2}\leq0$,
∴$-(x-1)^{2}+17\leq17$,
即多项式有最大值，且最大值为 17；
(3)$x^{2}-4x+5＞-x^{2}+4x-4$;
理由如下:
$x^{2}-4x+5-(-x^{2}+4x-4)$
$=x^{2}-4x+5+x^{2}-4x+4$
$=2x^{2}-8x+9$
$=2(x^{2}-4x+4-4)+9$
$=2(x-2)^{2}+1$;
∵$2(x-2)^{2}\geq0$,
∴$2(x-2)^{2}+1＞0$,
即$x^{2}-4x+5＞-x^{2}+4x-4$.