《2025年学习之友八年级数学上册人教版》

1. 下列图形中是轴对称图形的是(C)

答案： C

2. 在平面直角坐标系中,点$A(-4,2)$关于y轴对称点B的坐标为(B)
A.$(-4,2)$
B.$(4,2)$
C.$(4,-2)$
D.$(-4,-2)$

答案： B

3. 如图$m// n$,点$A在直线m$上,以$A为圆心的圆弧与直线n$,$m相交于C$,$B$两点.若$\angle CAB= 30^{\circ}$,则$\angle ABC$的度数为(D)

A.$45^{\circ}$
B.$60^{\circ}$
C.$70^{\circ}$
D.$75^{\circ}$

答案： D

4. 如图,在平面直角坐标系中,点$A的坐标是(2,0)$,点$B的坐标是(0,3)$,以$AB$为腰作等腰三角形,则在坐标轴上的另一个顶点有6个.

答案： 6

5. 如图已知$OA= a$,$P是射线ON$上一动点,$\angle AON= 60^{\circ}$,当$OP= $a时,$\triangle AOP$为等边三角形.

答案： a

6. 如图,$\triangle ABC$中,$AB= AC$,点$D$,$E$,$F分别在BC$,$AB$,$AC$上,且$BD= CF$,$BE= CD$,$G是EF$的中点,求证：$DG\perp EF$.

答案： 证明:连接ED,DF.
∵AB=AC,
∴∠B=∠C.在△BED和△CDF中,BE=CD,∠B=∠C,BD =CF,
∴△BDE≌△CFD(SAS),
∴DE=DF.
∵G是EF的中点,
∴DG⊥EF.

1. 一个等腰三角形的两边长分别是$4$,$8$,则它的周长为(C)
A.$12$
B.$16$
C.$20$
D.$16或20$

答案： C

2. 如图,在等边$\triangle ABC$中,$D是AB$的中点,$DE\perp AC于E$,$EF\perp BC于F$,已知$AB= 8$,则$BF$的长为(C)

A.$3$
B.$4$
C.$5$
D.$6$

答案： C

3. 如图所示,一艘海轮位于灯塔$P的北偏东30^{\circ}$方向,距离灯塔$4海里的A$处,该海轮沿南偏东$30^{\circ}$方向航行4海里后,到达位于灯塔$P的正东方向的B$处.

答案： 4

4. 如图,在$\triangle ABC$中,$\angle C= 90^{\circ}$,$\angle ABC= 60^{\circ}$,$BD平分\angle ABC$,若$AD= 6$,则$AC= $9.

答案： 9

5. $\triangle ABC$在平面直角坐标系中的位置如图所示.

(1)作出$\triangle ABC关于y轴对称的\triangle A_{1}B_{1}C_{1}$,并写出$\triangle A_{1}B_{1}C_{1}$各顶点的坐标；
(2)求$\triangle ABC$的面积；
(3)将$\triangle ABC向右平移6$个单位,作出平移后的$\triangle A_{2}B_{2}C_{2}$,并写出$\triangle A_{2}B_{2}C_{2}$各顶点的坐标；
(4)观察$\triangle A_{1}B_{1}C_{1}和\triangle A_{2}B_{2}C_{2}$,它们是否关于某直线对称？若是,请在图上画出这条对称轴.

答案：

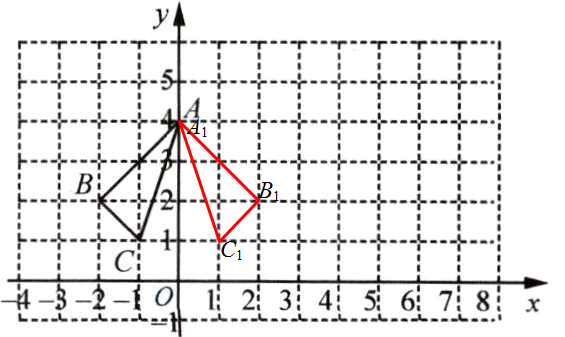
(1)A₁(0,4),B₁(2,2),C₁(1,1);
(2)S△ABC=2×3−$\frac{1}{2}$×1×1−$\frac{1}{2}$×1×3 −$\frac{1}{2}$×2×2=2 ;
(3)A₂(6,4),B₂(4,2),C₂(5,1);
(4)△A₁B₁C₁与△A₂B₂C₂关于直线l对称.